Home  │ Audio Home Page

Copyright © 2008, 2009, 2010, 2011, 2014, 2015
Updated November 28, 2015.  See document history at end for details.
SPICE verified where indicated.

Phono Equalization Calculations

 

Maximize your browser to allow room for the equations.  Verified on Internet Explorer and Firefox browsers.

The s variable will represent seconds or the Laplace s-domain variable according to context.

Table of Contents

• Introduction
• A Word Concerning Gain
• Inverting RIAA Network
• Non-inverting RIAA Network with Extra Zero
• Passive RIAA Network
• Passive RIAA Network with Extra Zero
• Two-Stage RIAA Equalization
• Current Input Networks
  

Introduction

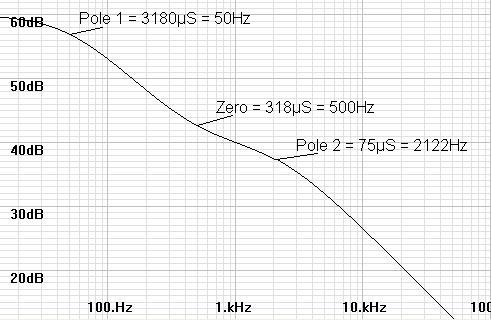
The intention of this document is to give the audio hobbyist mathematical basis to calculate the resistor and capacitor values in the RIAA equalization network of a phono preamp.  I searched the internet for this same information and could not find it.  As a result my curiosity compelled me to make the calculations myself.  The bode plot shown is of typical equalization curve with poles at 3180µs and 75µs, and a zero at 318µs.  A Gain of 60dB at DC and 40dB at 1kHz is typical of a MM voltage amplification stage.  Many hold that an additional zero at 3.18µs will compensate for a corresponding pole used in phono cutting amplifiers to put a practical limit on the pre-equalization gain at 50kHz.

Typical RIAA Equalization Bode Plot

The design cycle involves initially calculating capacitances from resistors appropriate for the desired gain and noise, rechoosing the nearest appropriate standard capacitor values in the correct ratio, then recalculating the resistances from which the nearest standard values are chosen.  This is because resistors are available in tighter tolerances than are capacitors.

I presume for now that you know how to set the gain for these circuits and that calculating the RC networks are the difficult calculation.

Op amps are used for ease of illustration only.  There is no intent to disparage discrete circuit designs.

A Word Concerning Gain

Most calculations are done with regard to low frequency gain (<50Hz).  Gain at 1kHz is roughly 1/10 (-20dB) that of low frequency gain.  Although you can work well with this ratio, if you desire to set an exact gain at 1kHz use the following ratios instead.

AV-1kHz AV<50Hz	=	0.10103	(-19.911018dB)
AV<50Hz AV-1kHz	=	9.89808	(19.911018dB)

In this context, you normally would set an exact 1kHz gain and multiply by 9.89808 to get the low frequency gain needed for calculations.

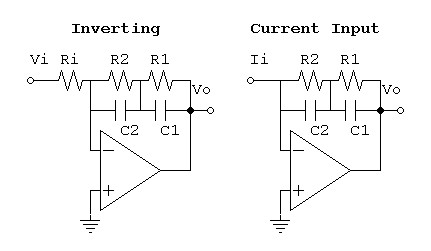
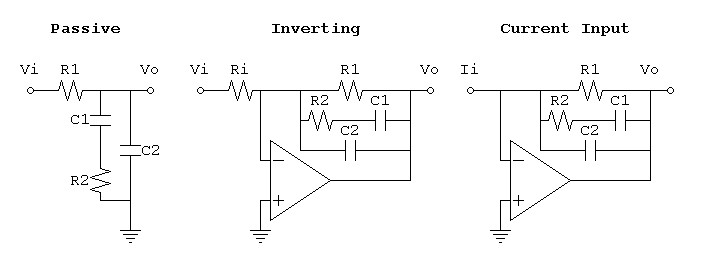
Inverting RIAA Network

(Series-Parallel)

 

Application

 

This calculation applies to an RIAA impedance network that converts unequalized signal current into equalized output voltage.  This includes inverting and current input stages.

 

Summary

 

 

T_P1 = R₁C₁ = 3180µs
T_P2 = R₂C₂ = 75µs
T_Z = (R₁||R₂)(C₁+C₂) = 318µs

T_Z is met when:
R₁/R₂ ratio = 11.78
and when C₁/C₂ ratio = 3.6

Inverting series-parallel version verified by SPICE:  Model.

 

Derivation

(1)

Z = R1||(1/sC1) + R2||(1/sC2) =

1 1/R1 + sC1

+

1 1/R2 + sC2

=

R1 sR1C1+1

+

R2 sR2C2+1

(2)

Z =

sR1R2C2 + R1 + sR1R2C1 + R2 (sR1C1 + 1)(sR2C2 + 1)

Time constant of reduced term is seen in (sT + 1).

Poles are clear, solve for zero.

(3)	sR1R2C2 + R1 + sR1R2C1 + R2 = s(R1R2C2 + R1R2C1) + (R1 + R2)

(4)

TZ =

R1R2C2 + R1R2C1 R1 + R2

=

R1(75µs) + R2(3180µs) R1 + R2

= 318µs

(5)	R1(75µs) + R2(3180µs) = (R1+R2)318µs

(6)	R1(75µs-318µs) + R2(3180µs-318µs) = 0

(7)

R1 R2

=

3180µs – 318µs 318µs - 75µs

= 11.777... = 11.7

(8)

C1 C2

=

TP1/R1 TP2/R2

=

3180µs/11.7R2 75µs/R2

= 3.6

 

Non-inverting RIAA Network with Extra Zero

(Series-parallel with extra zero)

 

Application

This calculation applies to an RIAA impedance network typical of non-inverting phono preamplifiers.  However it can also be used for inverting and current input applications.  An extra zero at 3.18µs requires an extra resistor making it the only network correcting an extra pole alleged to set a practical gain limit in some disk cutters.  With a zero at 3.18µs (50kHz) the minimum DC gain is 47dB for the non-inverting circuit.  It is worth noting that the non-inverting circuit will always have an extra zero whether you set it to 50kHz or to a maximum frequency.  It will be necessary to follow the non-inverting circuit with a first-order lowpass filter of same pole frequency as the undesired zero if you would be rid of it.
 

Summary

 

 

T_P1 = R₁C₁ = 3180µs
T_P2 = R₂C₂ = 75µs
T_Z1 = 318µs
T_Z2 = 3.18µs
R₁, R₂, and R₃ in ratio 217.173913 : 17.67514356 : 1 will yield correct time constants for zeros if C₁ and C₂ are chosen to yield correct poles.

Set gain for non-inverting circuit by proportioning R₃ between its R_3a and R_3b parts.

R3b =

(235.8490566)R3 AV<50Hz

= (0.2382778)R3 for RIAA standard 40dB gain at 1kHz

Now obviously, R₃a = R₃ - R₃b.

SPICE model of Inverse RIAA signal generator based on this circuit is verified.  (Similar to swapping R_i and RIAA RC network in inverting op-amp circuit to get inverse function.  Poles become zeros, and zeros become poles keeping the same time constants).
Inverse RIAA Subckt, Model to Test Inverse RIAA  Subckt.

SPICE model of non-inverting series-parallel riaa circuit with extra zero verifying correct adjustments for gain.
SPICE Model

See Low-noise Hybrid Op-amp/Discrete Phono Preamp for a complete design example of this type.

Derivation

(1)

Z = R1||(1/sC1) + R2||(1/sC2) + R3 =

R1 sR1C1 + 1

+

R2 sR2C2 + 1

+ R3

(2)

Z =

sR1R2C2 + R1 + sR2R1C1 + R2 + (sR1C1 + 1)(sR2C2 + 1)R3 (sR1C1 + 1)(sR2C2 + 1)

(3)

Z =

sR1R2C2 + R1 + sR2R1C1 + R2 + (s2R1C1R2C2 + sR1C1 + sR2C2 + 1)R3 (sR1C1 + 1)(sR2C2 + 1)

(4)

Z =

sR1R2C2 + R1 + sR2R1C1 + R2 + s2R1C1R2C2R3 + s(R1C1R3 + R2C2R3) + R3 (sR1C1 + 1)(sR2C2 + 1)

(5)

Z =

s2R1C1R2C2R3 + s(R1R2C2 + R2R1C1 + R1C1R3 + R2C2R3) + (R1 + R2 + R3) (sR1C1 + 1)(sR2C2 + 1)

Time constant of reduced term is seen in (sT + 1).

Poles are clear, solve for zeros.

(6)	s2R1C1R2C2R3 + s(R1R2C2 + R2R1C1 + R1C1R3 + R2C2R3) + (R1 + R2 + R3) = 0

(7)	s2(3180µs)(75µs)R3 + s(R1(75µs) + R2(3180µs) + (3180µs)R3 + (75µs)R3) + (R1 + R2 + R3) = 0

(8)	s2(238.5n(S2))R3 + s((R1 + R3)(75µs) + (R2 + R3)(3180µs)) + (R1 + R2 + R3) = 0

(9)

s2

R3(238.5n(S2)) R1 + R2 + R3

+ s

(R1 + R3)75µs + (R2 + R3)3180µs R1 + R2 + R3

+ 1 = 0

(10)	= s2TZ1TZ2 + s(TZ1 + TZ2) + 1 = 0

(11)

TZ1TZ2 =

R3(238.5n(s2)) R1 + R2 + R3

= 1.01124n(s2)

(12)

R3 R1 + R2 + R3

= 4.24m

(13)	R3 = 4.24m(R1 + R2 + R3)

(14)	R1 + R2 + R3 = 235.8490566 R3

(15)	R1 + R2 = 234.8490566 R3

(16)

TZ1 + TZ2 =

(R1 + R3)75µs + (R2 + R3)3180µs R1 + R2 + R3

= 321.18µs

(17)	(R1 + R3)75µs + (R2 + R3)3180µs = (R1 + R2 + R3)321.18µs

(18)	R1(75µs - 321.18µs) + R2(3180µs - 321.18µs) + R3(75µs + 3180µs - 321.18µs) = 0

(19) R₁(-246.18µs) + R₂(2858.82µs) + R₃(2933.82µs) = 0

(19)	R1(-246.18µs) + R2(2858.82µs) + R3(2933.82µs) = 0

The two equations (15) and (19) in three variables suggest R₁, R₂, R₃ variable but in fixed ratio as intuition would suggest.

Choose R₃ = 1 to solve for this ratio.
 
Then equation (15) becomes:
(20) R₁ + R₂ = 234.8490566

Then equation (19) simplifies to:
(21) R₁(-246.18µs) + R₂(2858.82µs) = -2933.82µs

Using simultaneous linear equations (18) and (19), solve for R₁ and R₂:

(22)

Det =

1 -246.18µ

1 2858.82µ

= 2858.82µ - -246.18µ = 3105µ

(23)

R1 =

234.8490566 -2933.82µ 1 2858.82µ 3105µ

=

(234.8490566)( 2858.82µ) - -2933.82µ 3105µ

(24)	R1 = 217.173913Ω

(25)

R2 =

1 -246.18µ 234.8490566 -2933.82µ 3105µ

=

-2933.82µ - (234.8490566)(-246.18µ) 3105µ

(26)	R2 = 17.67514356Ω

R₁, R₂, and R₃ in ratio 217.173913 : 17.67514356 : 1 will yield correct time constants for zeros if C₁ and C₂ are chosen to yield correct poles.

Set gain by proportioning R₃ between its R_3a and R_3b parts.

(27)

AV<50Hz =

R1 + R2 + R3a + R3b R3b

=

(217.173913 + 17.67514356 + 1)R3 R3b

=

(235.8490566)R3 R3b

Solve for R_3b to get final gain equation

(28)

R3b =

(235.8490566)R3 AV<50Hz

Passive RIAA Network

(Parallel)

Application

This calculation applies to an RIAA network normally used for passive equalization.  Parallel topologies are also preferred for discrete transistor designs because stray circuit capacitances can be compensated in C₂ and drain/collector resistances in R₁.  Application of Thevenin’s theorem moves R₁ into parallel with C₁ and R₂, opening up the use of the same network for inverting and current input applications.

Summary

T_P1 = 3180µs
T_P2 = 75µs
T_Z = 318µs = R₂C₁
R₁C₂ = 750µs
R₁C₁ = 2187µs
R₁:R₂ = 6.877358491
C₁:C₂ = 2.916

Passive parallel version verified by SPICE:  Model, Inverse RIAA Subckt used in model.

Derivation

(1)

Z = R1||(R2+(1/sC1)))||(1/sC2) =

R1 ||

sR2C1 + 1 sC1

||

1 sC2

(2)

Z =

1 1 R1 + sC1 sR2C1 + 1

||

1 sC2

=

1 s(R1C1 + R2C1) + 1 sR1R2C1 + R1

||

1 sC2

(3)

Z =

sR1R2C1 + R1 s(R1C1 + R2C1) + 1

||

1 sC2

=

1 s(R1C1 + R2C1) + 1 sR1R2C1 + R1 + sC2

(4)

Z =

1 s(R1C1 + R2C1) + 1 + s2R1R2C1C2 + sR1C2 sR1R2C1 + R1

(5)

Z =

sR1R2C1 + R1 s2R1R2C1C2 + s(R1C1 + R2C1 + R1C2) + 1

Zero is clear:

(6)

sTZ + 1 =

sR1R2C1 + R1 R1

, therefore TZ = R2C1 = 318µs

Solve for poles:

(7)	s2TP1TP2 + s(TP1 + TP2) + 1 = 0

(8) T_P1T_P2 = R₁R₂C₁C₂ = (R₂C₁)R₁C₂ = T_ZR₁C₂  (from equations (5) and (7))

(8)	TP1TP2 = R1R2C1C2 = (R2C1)R1C2 = TZR1C2  (from equations (5) and (7))

(9)

R1C2 =

TP1TP2 TZ

=

(3180µs)(75µs) 318µs

= 750µs

(10)	TP1 + TP2 = R1C1 + R2C1 + R1C2  (from equations (5) and (7))

(11)	3180µs + 75µs = R1C1 + 318µs + 750µs

(12)	R1C1 = 3180µs + 75µs - 318µs - 750µs = 2187µs

(13)

R1 R2

=

R1C1 R2C1

=

2187µs 318µs

= 6.877358491

(14)

C1 C2

=

R1C1 R1C2

=

2187µs 750µs

= 2.916

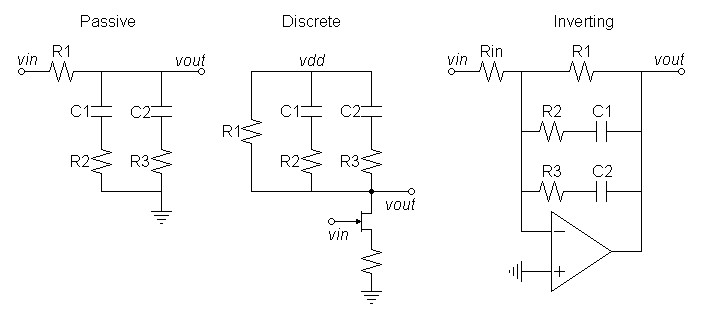
Passive RIAA Network with Extra Zero

(Parallel)

Application

This calculation adds an extra 50kHz zero to an RIAA network normally used for passive equalization.  Parallel topologies are also preferred for discrete transistor designs because stray circuit capacitances can be compensated in C₂ and drain/collector resistances in R₁.  The addition of R₃ in series with C₂ to add the extra zero somewhat diminishes this advantage, complicating the compensation for stray capacitance.  Application of Thevenin’s theorem moves R₁ into parallel with C₁ and R₂, opening up the use of the same network for inverting and current input applications.

Summary

T_P1 = 3180µs
T_P2 = 75µs
T_Z1 = R₂C₁ = 318µs
T_Z2 = R₃C₂ = 3.18µs
R₁C₁ = 2209.09µs
R₁C₂ = 724.73µs
Resistors R₁, R₂, and R₃ are in ratio 227.902:32.8066:1

Passive parallel version verified by SPICE:  Model, Inverse RIAA Subckt used in model.

Derivation

(1)

Z = R1 || (R2+1/sC1) || (R3 + 1/sC2) = R1 ||

sR2C1+1 sC1

||

sR3C2+1 sC2

(2)		1		1
	Z =		=
		1 R1 + sC1 sR2C1+1 + sC2 sR3C2+1		(sR2C1+1)(sR3C2+1) + sR1C1(sR3C2+1) + sR1C2(sR2C1+1) R1(sR2C1+1)(sR3C2+1)

(3)		R1(sR2C1+1)(sR3C2+1)		R1(sR2C1+1)(sR3C2+1)
	Z =		=
		(s2R2R3C1C2 + s(R2C1+R3C2) +1) + (s2R1R3C1C2 + sR1C1) + (s2R1R2C1C2 + sR1C2)		s2(R2R3C1C2+R1R3C1C2+R1R2C1C2) + s(R2C1+R3C2+R1C1+R1C2) + 1

Zeros are clear:
T_Z1 = 318µs = R₂C₁
T_Z2 = 3.18µs = R₃C₂

Solve for poles in form of

(4)	s2TP1TP2 + s(TP1+TP2) + 1 = 0

where

(5)	TP1TP2 = R2R3C1C2 + R1R3C1C2 + R1R2C1C2 = TZ1TZ2 + TZ2R1C1 + TZ1R1C2

(6)	TP1+TP2 = R2C1 + R3C2 + R1C1 + R1C2 = TZ1 + TZ2 + R1C1 + R1C2

Let T_A = R₁C₁, T_B = R₁C₂,  T_P1 = 3180µs, T_P2 = 75µs and setup simultaneous linear equations for T_A and T_B:

From equation (5)
T_Z2T_A + T_Z1T_B = T_P1T_P2 - T_Z1T_Z2
3.18µT_A + 318µT_B = (3180µ × 75µ) - (318µ × 3.18µ) = 238.5n - 1.01124n

(7)	3.18µTA + 318µTB = 237.489n

From equation (6)
T_A + T_B = T_P1 + T_P2 - T_Z1 - T_Z2 = 3180µ + 75µ - 318µ - 3.18µ

(8)	TA + TB = 2.93382m

Using simultaneous linear equations (7) and (8), solve for T_A and T_B:

(9)

Det =

3.18µ 1

318µ 1

= 3.18µ – 318µ = –314.82µ

(10)

TA =

237.489n 2.93382m 318µ 1 –314.82µ

=

237.489n – (318µ)(2.93382m) –314.82µ

(11)	TA = 2209.09µs = R1C1

(12)

TB =

3.18µ 1 237.489n 2.93382m –314.82µ

=

(3.18µ)(2.93382m) – 237.489n –314.82µ

(13)	TB = 724.73µs = R1C2

(14)

R1 R3

=

TB TZ2

=

724.73µs 3.18µs

=

227.902

(15)

R1 R2

=

TA TZ1

=

2209.09µs 318µs

=

6.94682

(16)

R2 R3

=

R1/R3 R1/R2

=

227.902 6.94682

=

32.8066

Resistors R₁, R₂, and R₃ are in ratio 227.902:32.8066:1

Two-Stage RIAA Equalization

Application

Sometimes it is desireable to divide the equalization between two stages.  All practical circuits put the 3180µs pole and the 318µs zero in one stage leaving the 75µs pole to the other.

Circuit 1:  Series/Parallel

Summary

T_P1 = R₁C₁ = 3180µs
T_Z1 = (R₁ || R₂)C₁ = 318µs
R₁ = 9 × R₂
R₂ = R₂a + R₂b for non-inverting circuit

Derivation

 (1) Z = R₂ + (R₁||(1/sC₁))

(2)		R1 sC1		R1		sR1R2C1 + R1 + R2
	Z = R2 +		= R2 +		=
		R1 + 1 sC1		sR1C1 + 1		sR1C1 + 1

 (3) T_P1 = R₁C₁ = 3180µs

(4)

TZ1 =

R1R2C1 R1 + R2

= (R1 || R2)C1 = 318µs

Combine equations (3) and (4):
(5) T_Z1 x 10 = T_P1
(6) (R₁ || R₂)C₁ x (T_P1/T_Z1) = R₁C₁
(7) (R₁ || R₂) x (T_P1/T_Z1) = R₁

(8)	(TP1/TZ1)
		= R1
	1 R1  + 1 R2

(9)

1 R1

+

1 R2

=

(TP1/TZ1) R1

, therefore

1 R2

=

(TP1/TZ1) – 1 R1

(10)

R1 =

TP1 TZ1

– 1

R2

Substituting back T_P1/T_Z1 = 10 into equation 10 gives
(11) R₁ = 9 × R₂

Circuit 2:  Parallel/Series

Summary

T_P1 = (R₂ + R₁)C₁ = 3180µs
T_Z1 = R₁C₁ = 318µs
R₂ = 9 × R₁

Derivation

 (1) Z = R₂ || (R₁ + 1/sC₁)

(2)		R2 R1 + 1 sC1		sR2R1C1 + R2
	Z =		=
		R2 + R1 + 1 sC1		s(R2 + R1)C1 + 1

 (3) T_P1 = (R₂ + R₁)C₁ = 3180µs

(4)

TZ1 =

R2R1C1 R2

= R1C1 = 318µs

Combine equations (3) and (4):
(5) T_P1 =10T_Z1
(6) (R₂ + R₁)C₁ = (T_P1/T_Z1) × R₁C₁
(7) R₂ + R₁ = (T_P1/T_Z1) × R₁

(8)

R2 =

TP1 TZ1

– 1

R1

Substituting back T_P1/T_Z1 = 10 into equation 8 gives
 (9) R₂ = 9 × R₁

75µs Lowpass Stage Common to Both

Summary

T_P2 = R₃C₃ = 75µs
 

If you have comments on the calculations email me at contact@waynestegall.com

Current Input Networks

Application

 

The RIAA equalization calculations above presume that no equalization is needed for the input loop itself.  For voltage input designs, correct RC loading at the preamp input meet these conditions, although not perfectly.  Reading reviews of current input designs did not mention any special compensation that I remember.  However when I reexamined this issue I found the following result:  The virtual short at the input reduces the equivalent input loop to a RL response with a low cutoff frequency, which would greatly attenuate the treble.  This is because the complex pole pair of the full second order circuit diverges into two real poles below a Q of 0.5 (The second pole is pushed far into the ultrasonic region with the Q values involved). Therefore it is necessary to add a zero of the same value to the compensation circuit, perhaps in a second stage.  I present this result only after I verified it by examining a patent for this type of circuit issued in 1984 (That it expired 17 years later in 2001 makes this a public domain design.)  Because in the winding of an inductor both R and L increase with the number of turns, cartridges whose windings are made with the same gauge magnet wire may all have the same or similar RL response.  This suggests the selection of a fixed compensation zero as a design compromise.  Others may want to have an adjustable zero to tailor the compensation to their desired cartridge.

Summary

Time constant and frequency of pole of cartridge RL response and therefore of required compensation zero:

TZ3 =

L R

fZ3 =

R 2πL

The circuit shown is recommended because it allow adjustable compensation zero to be place in either stage without the adjustment affecting the value of the poles.

Recommended circuit allows placement of compensation in either stage.

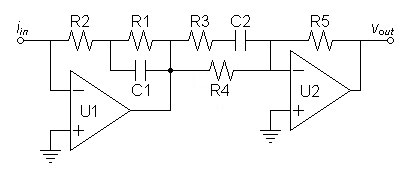Design equations

For first stage cartridge compensation zero adjusted by R₂:

first stage:
T_P1 = R₁C₁ = 3180µs
T_Z1 = (R₁ || R₂)C₁ = T_Z3

R1 =

3180µs TZ3

– 1

R2

second stage:
T_Z2 = (R₃ + R₄)C₂ = 318µs
T_P2 = R₃C₂ = 75µs
R₄ = 3.24 × R₃

Verifying SPICE model.
Reverse RIAA subcircuit used with all models.

For second stage cartridge compensation zero adjusted by R₄:

first stage:
T_P1 = R₁C₁ = 3180µs
T_Z1 = (R₁ || R₂)C₁ = 318µs
R₁ = 9 × R₂

second stage:
T_Z2 = (R₃ + R₄)C₂ = T_Z3
T_P2 =  R₃C₂ = 75µs

R4 =

TZ3 75µs

– 1

R3

Verifying SPICE model.
Reverse RIAA subcircuit used with all models.

In either case the low frequency transimpedance gain is the same.

ZGAIN =

(R1 + R2)R5 R4

Which version to choose?

My first instinct was to place the compensation adjustment in the second stage because a potentiometer would contribute less scratch noise there.  The drawback is that the adjustment of R₄ stands to alter the gain in direct proportion to the alteration in compensation turnover frequency.  However, if the compensation zero is placed in the first stage the adjustment of R₂ does not stand to alter the gain much so long as the expected condition (R₁ >> R₂) holds.  If the scratching of potentiometers is unwanted in high gain circuits perhaps stepped attenuators should be used with the stipulation that adjustments be made with the preamplifier offline.

Other topologies

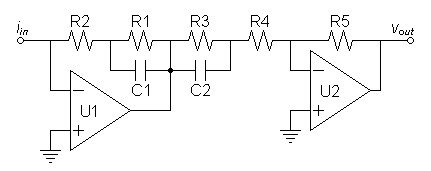
The first topology was given to allow the adjustable zero to be placed in either stage.  However the stage with the fixed zero does not have to be that first given and choosing the alternative gives the additional circuits below.  Particularly note that the discrete circuit prefers the series-parallel topology for both stages so that R₄ can compensate for the transistor output impedance's effect on the second stage network.

Series-Parallel in both stages allowed by adjustment in first stage

Discrete Full Series-Parallel Circuit

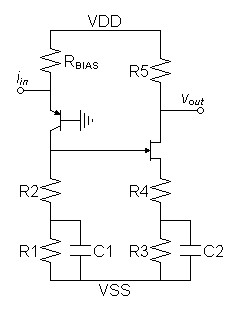Note:  Incomplete schematic only illustrates equalization topology, biasing is likely incorrect

Design equations

For first stage cartridge compensation zero adjusted by R₂:

first stage:
T_P1 = R₁C₁ = 3180µs
T_Z1 = (R₁ || R₂)C₁ = T_Z3

R1 =

3180µs TZ3

– 1

R2

second stage:
T_Z2 = R₃C₂ = 318µs
T_P2 = (R₃ || R₄)C₂ = 75µs
R₃ = 3.24 × R₄

Verifying SPICE model.
Reverse RIAA subcircuit used with all models.

Parallel-Series in both stages allowed by adjustment in second stage

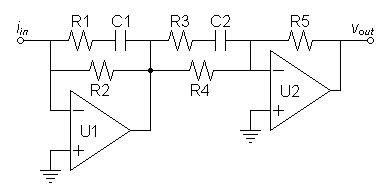For second stage cartridge compensation zero adjusted by R₄:

first stage:
T_Z1 = R₁C₁ = 318µs
T_P1 = (R₁ + R₂)C₁ = 3180µs
R₂ = 9 × R₁

second stage:
T_Z2 = (R₃ + R₄)C₂ = T_Z3
T_P2 =  R₃C₂ = 75µs

R4 =

TZ3 75µs

– 1

R3

Verifying SPICE model.
Reverse RIAA subcircuit used with all models.

Yet more

After giving these additional topologies, more can be specified by swapping the stage 1 network of R₁, R₂, and C₁ with R₅.  By moving all equalization to the second stage the first stage then gives straight preliminary gain.  This approach may be favored for lower noise by the fact that the current-input signal may have much flatter frequency response than that of a voltage input signal as shown the following plot.

Current-input equalization at a plausibly typical cartridge LR frequency of 212.2Hz shows much flatter equalization than voltage input designs.

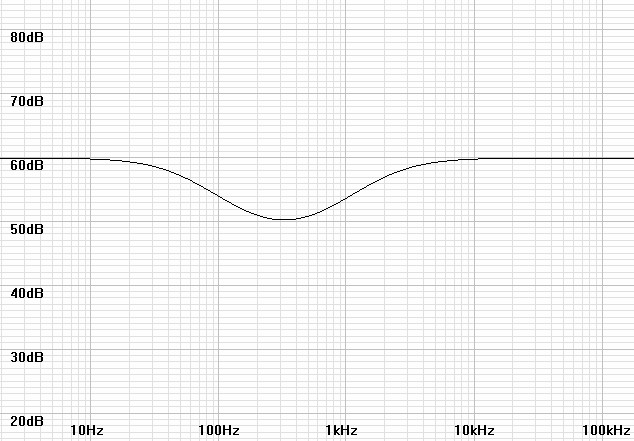Derivation

The derivation of the design equations from the topology and Laplace equations is the same as that for the Two-Stage RIAA Equalization given above.  Indeed, the first stage is exactly the same as that of the series-parallel first stage given before.  The second stage has a parallel-series RC component on the input side of the op-amp where it was in the feedback loop of the first stage parallel-series that came before thus inverting the transfer equation.  This converts poles to zeros and zeros to poles but otherwise the calculations remain the same with minor differences.



Document History:
? 2008  Creation
October 24, 2009  Corrected typo in equation (3b) of Calculating Passive RIAA Equalization
May 7, 2010  Corrected capacitor ratio of Passive RIAA network in summary to match result of calculations.
June 2, 2010  Added two-stage RIAA calculations.
June 22, 2010  Corrected calculations for Calculating Non-inverting RIAA Network with Extra Zero (Series-parallel with extra zero) and verified with SPICE.  Verified others with SPICE as well and provided models where indicated.  Delete incomplete example at end.  All calculations for circuits in this document are deemed correct and verified at this time except that full current input calculations have not been developed.
July 5, 2010  Added section detailing adjustments for exact 1kHz gain relative to that which is approximate.
July 6, 2010  Removed reference to an error corrected long ago.
September 16, 2010  Corrected isolated error in equation (9) of Calculating Non-inverting RIAA Network with Extra Zero that did not affect results because the correct value was carried forward in the calculations instead.  In same section make additional calculations to correct incorrect gain presumptions.  (SPICE had correctly verified equalization but not gain :-\ )
October 29, 2010  Added link to design example.
March 23, 2011  Added Passive RIAA network with extra zero.
March 23, 2011  Changed second unit from S to s to distinguish it from conductance unit, made other minor improvements.
February 6, 2014  Added schematic and design equations for op-amp based current-input circuit.
March 17, 2014  Expanded derivation of two stage equalization equations to more easily show how current-input equalization derives from them.  Added more topologies and detail for current input designs.
November 28, 2015  Improved formatting.