Copyright © 2010

Created January 2, 2010
Updated January 27, 2010.  See document history at end for details.

Active Inductor Example

JFET Phono Preamp

This is an example only.  It is not intended to be final or complete design.

Figure 1:  Schematic

Parts List Q1-Q4 2N3918 n-ch jfet Q5,Q6 BS170 n-ch mosfet R1,R3,R5,R7 220Ω, 5% R2,R4,R6,R8 220Ω, 5% R2L 165kΩ, 1% R2N 23.7kΩ, 1% C1N,a 13nF, 1% or 5% C1N,b 240pF, 1% or 5% C2N,a 4.3nF, 1% or 5% C2N,b 240pF, 1% or 5% R1L 105kΩ, 1% CL 10,000µF, 25V electrolytic R9,R11 1kΩ, 5% R12 82Ω, 5% R13 1kΩ, 5% C2 100µF, 25V electrolytic R15 1kΩ pot S1,S2 SPST reed relay, normally closed, coil rated 10mA@5V Remaining values are left for you to calculate.  See text.

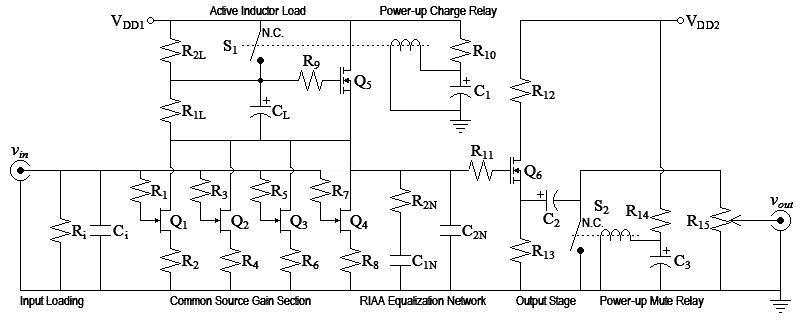Initial Design Decisions

• Discrete voltage input design with 46db gain at 1kHz will amplify 5mV rms input to produce 1V rms before attenuator.
  
• Q₁-Q₄ are 2N3918 n-ch jfet (6nV/rtHz noise is not bad, you may choose a better device)
• I chose four devices because multiple parallel devices increase S/N by sqrt(# of devices).  In this case the effective noise specification is bettered to 3nV/rtHz.
• Q₅,Q₆ are BS170 n-ch mosfet (commonly available)
• v_gs,max of Q₆ of 20V limits V_DD due to startup relays.  Choose V_DD = 18V.
• Let bias of active inductor set bias to gate of Q6 to eliminate coupling capacitor.

vg,Q5 =

(VDD-vgs-Q5-max)+vsg-Q1-max 2

=

18V-2V+8V 2

= 12V

• R_2L of active inductor functions as R₁ of passive RIAA network.
• I chose to do the small signal class-a design with a fourier series based distortion predictor tool out of convenience.  Small signal class-a design is not in the scope of this article.
• Because of possibility of negative feedback from buffer stage back to gain stage through power supply, I decided to recommend two power supply taps.
  

Gain Stage Design

Although I used a convenient fourier series analysis tool to do the small signal analysis, there were some design decisions.  I wanted to choose gate and source resistors small enough to make their noise contribution insignificant compared to the JFET.  This would lower noise and allow the possiblity of noise improvement with better JFETs.

Resistor noise equation (per rtHz, figure of merit, does not account for bandwidth)

vn-resistor-rtHz = sqrt(4kTR)

Rearrange resistor noise equation to calculate equivalent input noise resistance of JFET.

R =

vn-resistor-rtHz2 4kT

=

6nV2 4 x 1.3806504e-23 x 298.15ºK

= 2.186371576kΩ

I choose R_G and R_S 10 times lower to make their noise contribution insignificant.
R1-R8 = 220Ω.
Because the fourier series analysis resulting from this choice was excellent, I made no further adjustments to these values.

Fourier Series Analysis of Q₁-Q₄ (excluding drain load)

Analysis of Common Source Circuit
transistor type = JFET
transconductance = 5.5mS
threshold voltage = -3V
source resistor = 220Ω

Input signal (peak) = 7.0710678mV
Input bias = 0V
Output signal (peak) = 21.585572µA
Output bias = 7.8662828mA¹
Gain = 3.0526609mS

Total distortion = 1.6210607nA = 0.00750993% = -82.4873dB

Breakdown by harmonic

harmonic	value	percent	dB
0	7.8662844mA1	36442.32534044%	51.23dB	DC Offset
1	21.585572µA	100.00000000%	0.00dB	Fundamental
2	1.6210607nA	0.00750993%	-82.49dB

RIAA Analysis

Refer Calculating Passive RIAA Equalization in article Phono Equalization Calculations.

From this fourier analysis we can calculate R₁ of Passive RIAA network (aka R_2L)

R2L =

(Low frequency RIAA boost relative to 1kHz) x (1kHz output voltage) (Output signal current) x (#parallel devices)

=

10 x 1.414213562V 21.585572µA x 4

= 163.791532kΩ

Round to nearest 1% value.  R_2L = 165kΩ

Given R₁:R₂ = 6.877358491

R2N =

165kΩ 6.877358491

= 23.99176955kΩ

Round to nearest 1% value.  R_2N = 23.7kΩ

Given R₁C₁ = 2187µS

C1N =

2187µS 165kΩ

= 13.25454545nF

Round down to nearest 5% value: 13nF
Choose parallel 5% value to makeup remainder:  240pF
C_1N = 13nF + 240pF

Given R₁C₂ = 750µS

C2N =

750µS 165kΩ

= 4.545454545nF

Round down to nearest 5% value: 4.3nF
Choose parallel 5% value to makeup remainder:  240pF
C_2N = 4.3nF + 240pF

Active Inductor Analysis

Refer article Active Inductor Load.

• Choose R_2L for gain of overall circuit.

R_2L chosen already in RIAA analysis.

• Calculate/set g_fs in preparation for remaining calculations, verifying bounds of equation (22). (equation (9))

BS170 specification:  g_m = 320mS.
g_fs = 2 x sqrt(g_mi_D) = 2 x sqrt(320mS x 7.8662828mA x 4) = 200.6872391mS

• Choose R_1L to set desired DC bias.  (equation (24))

R1L =

R2L Vbias vT+sqrt(iD/gm) -1

=

165kΩ 6V 2V+sqrt((7.8662828mA x 4)/320mS) -1

= 103.5527796kΩ

Round to nearest 1% value:  R_1L = 105kΩ

• Choose C_L to set the pole frequency the desired amount below the passband.  (equation (21))

CL =

gfsR1L+1 2πfPOLER1L

=

(200.6872391mS x 105kΩ)+1 2π x 5Hz x 105kΩ

= 6.388376376mF

6800µF would work here.  I would rather choose a larger common value (C_L = 10,000µF) and solve for a lower pole.

fPOLE =

gfsR1L+1 2πCLR1L

=

(200.6872391mS x 105kΩ)+1 2π x 10mF x 105kΩ

= 3.194188188Hz

• Determine if a bypass switch is needed to charge the capacitor on startup.

Power on relay added at beginning of design.
Calculate charge time for C_L:

i = C

δv δt

Rearrange capacitor equation above and calculate time.  (2V presumes v_gs not much more than v_T)

Δt =

CΔv iD

=

10mF x 2V 7.8662828mA x 4

= 635.6242366mSec

Q₆ Circuit Design

My design goal here was reasonably low output impedance.  1kΩ output impedance would have been low enough to minimize voltage loss into a typical 47kΩ load.  I choose 500Ω instead on the far chance of driving a 600Ω load with a tolerable voltage loss.

Fourier Series Analysis of Q₆ Circuit

Note:  This analysis based on a more convenient equivalent model of source circuit.  Two 500Ω are modeled in series with one bypassed by a capacitor in place of the parallel circuit shown.
Analysis of Common Source Circuit
transistor type = MOSFET
transconductance = 320mS
threshold voltage = 2V
source resistor = 500Ω

Input signal (peak) = 1.4142136V
Input bias = 7V
Output signal (peak) = 2.7910912mA
Output bias = 9.8041739mA¹
Gain = 1.9735995mS

Total distortion = 950.79116nA = 0.03406521% = -69.3538dB

Breakdown by harmonic

harmonic	value	percent	dB
0	9.805058mA1	351.29836800%	10.91dB	DC Offset
1	2.7910912mA	100.00000000%	0.00dB	Fundamental
2	888.84698nA	0.03184586%	-69.94dB
3	56.727241nA	0.00203244%	-93.84dB
4	4.7600566nA	0.00017054%	-115.36dB
5	456.88194pA	0.00001637%	-135.72dB

Miscellaneous Calculations

R₁₂ limits charge current through Q₆ to C₂ to <500mA
R₁₂ >= 20V/500mA = 40Ω
Choose R₁₂ = 82Ω.

Want to set C₂ for as low a highpass pole as C_L.  First find R_equiv of pole.  Output impedance of Q₆ is the inverse of its operating ac transconductance g_fs.
g_fs = 2 x sqrt(g_mi_D) therefore

Rout-Q6 =

1 2 x sqrt(gmiD)

=

1 2 x sqrt(320mS x 9.8041739mA)

= 8.92667066Ω

Requiv = (Rout-Q6 || R13) + R15 =

Rout-Q6 x R13 Rout-Q6 + R13

+ R15 = 1.00884769kΩ

C2 =

1 2πfpoleRequiv

=

1 2π x 2.348779238Hz x 1.00884769kΩ

= 67.16643973µF

Choose C₂ = 100µF.

Choose R₁₀ and  R₁₄ to set 10mA through relay coil.

R10 =

VDD-vCOIL iCOIL

=

18V-5V 10mA

= 1.3kΩ

Calculate load current from power supplies V_DD1 and V_DD2.
i_DD1 = i_Q1-BIAS x 4 + i_RELAYCOIL = 7.8662828mA x 4 + 10mA  = 41.4651312mA
i_DD2 = i_Q6-BIAS + i_{RELAYCOIL =} 9.8041739mA + 10mA = 19.8041739mA

Design Decisions Left to You

• Ri and Ci should be calculated per article Phono Termination Calculations and Calculator.
• Gate resistors were somewhat arbitrarily chosen.  They seem to be good values.  I know that the 1kΩ values work with the BS170.  I have seen many jfet schematics without gate resistors at all.  Increase them if any oscillations occur.
• Relay components C₁ and C₃ must be calculated as follows:

C₁ must be chosen by calculation or experimentation to exceed C_L charge time calculated above (432.2244809mSec).  C₃ would then be chosen for a somewhat longer delay to prevent a pop from the activation of the other relay.

• This circuit and its analysis is only given as an example; change everything if you like.
• A low noise 18V power supply.  I recommend the circuit of article Line Level Class A Power Supply.
  

¹There is a seeming discrepancy in the fourier analysis between the cited output bias and the same value given in the analysis.  The first value is the bias without any signal and the second with a signal. This effect is created by the same asymetrical transfer curve that gives us a desireable second order distortion characteristic.  The positive half of the signal is amplified more than the negative half.  As a result the dc bias is modulated by the average signal level. This small component amounts to AM demodulation of the  music signal.  Abstractly, I had already anticipated this effect.  I would be curious what effect this has on the overall sound.  Is is detrimental, or does it add an extra euphonic bass urge?

Document History
January 2, 2010  Created
January 2, 2010  Minor Updates.
January 5, 2010  Recommend split power supply to prevent feedback.  Update schematic to show change.  Recommend specific power supply.
January 5, 2010  Choose relays S1 and S2, calculate their series resistors, and calculate specific load current for each power supply tap.
January 9, 2010  Added footnote explaining how fourier series analysis shows modulation of dc bias by music signal.
January 17, 2010  Added design criteria for class-a biasing decisions.  Recalculate Active Inductor Analysis due to miscalculation of g_fs.
January 23, 2010  Correct schematic in vicinity of Q₄, R₇, and R_2N.
January 27, 2010  Minor improvement to writing style.