Home  │ Audio Home Page

Copyright © 2010 by Wayne Stegall
Updated March 26, 2011.  See document history at end for details.

Low-Noise Two-Stage JFET Phono Preamp

This circuit is SPICE verified.  It is only provided for design assistance.  Its final validity awaits someone to prototype it.

Figure 1:  Schematic

Parts List * R1 47kΩ, 1/8V * C1 100pF, metal film Q1-Q5 LSK170A n-ch jfet Q6 LSK170C n-ch jfet R2,R3,R4,R5 56Ω, 5%, 1/8W R6 2kΩ, 1%, 1/2W ** C2a 39nF, 1% plastic film ** C2b 2.7nF, 1% plastic film C3 3.9µF polyethylene R7 10MΩ, 1%, 1/8W R8 442kΩ, 1%, 1/8W R9 1.1kΩ, 5%, 1/2W R10 2kΩ, 1%, 1/8W ** C4a 160nF, 1% plastic film ** C4b 16nF, 1% plastic film R11 18.2kΩ, 1%, 1/8W R12 2.4kΩ, 5%, 1/2W R13 2.4kΩ, 5%, 1/2W R14 100kΩ, 5%, 1/8W C5 10uF polyethylene or 180µF electrolytic, see text * Default values.  R1 and C1 should be calculated to match cartridge LCR per article Phono Termination Calculations and Calculator. 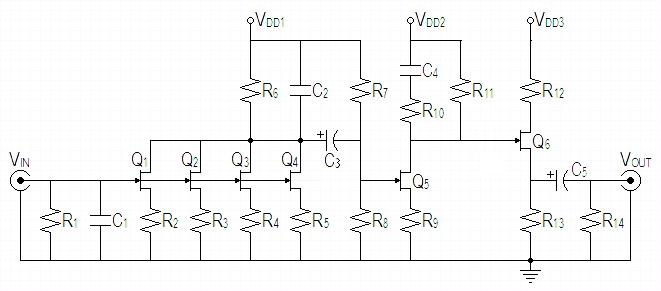** Capacitor pairs are connected in parallel. Verify parts list to final SPICE model.

Initial Design Decisions

• Design approach is to use higher voltage power supply to allow larger gain with conventional class A circuits.
• Want 5mV_RMS to produce 1V_RMS at output at 1kHz.  This amounts to 46dB of gain at 1kHz.  Most gain references and calculations are relative to 66dB of gain below 50Hz.  Altered gain goal to standard RIAA 40dB of gain at 1kHz to lower distortion.
• Initially choose 48V power supplies because of unsatisfactory results with 40V supply in prior design cycle.
• Q₁-Q₅ are LSK170A n-ch jfet (chosen for excellent 1nV/√Hz noise specification).  Use A grade for more possible gain.
• Desireable self bias (V_g-dc = 0V, all bias set by source resistor) on first stage is allowed by small input signal. (Signal will clip if peak is greater than  V_p0 of -0.4025156V; distortion considerations require even more headroom.)
• That a larger signal drives second stage requires more bias than self bias would allow.  Use gate biasing for second stage.
• I chose four devices for stage one because multiple parallel devices devices increase S/N by sqrt(# of devices).  In this case halving the effective noise in the source circuit and to some extent overall.
• Q₆ is LSK170C n-ch jfet.  Biasing concerns disadvantage MOSFET here.
• Because of possibility of negative feedback from buffer stage back to gain stage through power supply, I decided to recommend three power supply taps.

Figure 2:  Stage with 75µS pole (red curve) will boost signal out of noise quicker in first stage than one with 3180µS pole and  318µS zero (black curve).

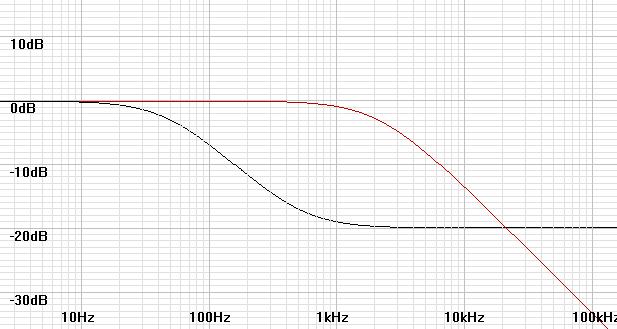Gain Stage Design

As an Initial observation, a higher gate bias in the second stage forced by the gain of the first stage would cause the first stage to bear a greater share of the overall gain.

Figure 3:  LSK170A SPICE model for reference

.MODEL LSK170A NJF + BETA   = 0.0378643       VTO    = -0.4025156      LAMBDA = 4.783719E-3        + IS     = 3.55773E-14      + RD     = 10.6565         RS     = 6.8790487                    + CGD    = 3.99E-11        CGS    = 4.06518E-11        + PB     = 0.981382        FC     = 0.5                + KF     = 0               AF     = 1

Stage One

I wanted to choose  source resistors small enough to make their noise contribution insignificant compared to the JFET.  This would lower noise and allow the possiblity of noise improvement with better JFETs.

Resistor noise equation (per √Hz, figure of merit, does not account for bandwidth)

vn-resistor-rtHz = sqrt(4kTR)

Rearrange resistor noise equation to calculate equivalent input noise resistance of JFET.

R =

vn-resistor-rtHz2 4kT

=

1nV2 4 x 1.3806504e-23 x 298.15ºK

= 60.73254378Ω

I would like to choose R_S much lower than 60Ω to make their contribution insignificant.  However, I believe a 6Ω source resistor would greatly raise distortion and bias for a small signal transistor.  Rather, instead I will match the source resistor to the JFET noise resistance.
R₂-R₅ = 56Ω.

Some initial conditions would allow direct computation of bias, but iteration (repetitive computer calculations) or a load line graph are required to calculate the current bias to begin small signal analysis from the parameters given (V_gs-dc = 0V and R_s = 56Ω).
Given k_n (BETA) = 37.8643mA/V² and V_T = -402.5156mV for LSK170A, bias current iterates to 2.551918mA.
Given LAMBDA = 4.783719m(V^-1) from LSK170A spice model calculate r_ds:

rds =

1 LAMBDA x  iD0

=

1 4.783719m(V-1) x 2.551918mA

=  81.9159kΩ

Anticipating V_DS biased at 4V maximum, add contribution of r_ds to effective I_D:

ID = 2.551918mA +

4V 81.9159kΩ

=

2.60075mA

Calculate g_fs and make a rough estimate of maximum possible gain to continue calculations.  (This is a situation where we need to know the gain before we actually calculate it.)
g_fs = 2 x sqrt(k_nI_D) = 2 x sqrt(37.8643mA/V² x 2.60075mA) = 19.8470mS

AV-preliminary =

Apparent max load bias voltage |VGS|

=

VDD - 2|VT-max| ID x (Rs + 1/gfs)

=

48V - 2(2V) 2.60075mA x (56Ω + 1/19.8470mS)

= 159.0273565(V/V)

Want drain load much less than r_ds/4  to minimize affect of parameter variance on equalization.  Calculate bias limit on R_d:

Rd  <=

VDD - (VG+|VT-max|) - (vg-peak x AV-preliminary) - (VDRAIN-SAFETY-FACTOR) ID x 4

=

48V - (0V + 2V) - (14mV x 159.0273565) - 4V 2.60075mA x 4

= 3.82328kΩ

Choose next lower 1% standard value:  R₆ = 3.74kΩ

We must know Input bias to second stage to finish calculations for first stage.
Make a more refined gain estimate for stage 1 to set stage 2 input bias:

AV-refined =

4 x Rd-total Rs + 1/gfs

=

4 x (R6 || (rds/4)) Rs + 1/gfs

=

4 x (3.74kΩ || 20.479kΩ) 56Ω + 1/19.8470mS

= 118.906(V/V)

Calculate peak signal to stage 2 from 14mV peak input:
v_{g-peak-stage2} = v_{g-peak-stage1} x 14mV = 118.906 x 14mV_peak = 1.66468V_peak

AV-stage2  =

AV-total AV-stage1

=

2000 118.906

= 16.82(V/V)

Vbias-stage2 =

VDD - |VT-max| -  vg-peak-stage2 - (VDRAIN-SAFETY-FACTOR) (AV-stage2 + 1) + AV-SAFETY-FACTOR

=

48V - 2V - 1.66468V - 4V 20

=  2.01677V

Try round down to V_bias-stage2 = 2V

Choose R₇ = 10MΩ, calculate R₈:

R8  = 10MΩ x

Vbias-stage2 VDD - Vbias-stage2

= 10MΩ x

2V 48V - 2V

= 434.783kΩ

Choose next higher 1% standard value:  R₈ = 442kΩ.
Calculate actual bias with standard values:

Vbias-stage2  =

48V x 442kΩ 10MΩ + 442kΩ

= 2.03179V

Calculate  final gain.

AV-stage1 =

4 x Rd-total Rs + 1/gfs

=

4 x (R6 || R7 || R8 || (rds/4)) Rs + 1/gfs

=

4 x (3.74kΩ || 10MΩ || 442kΩ || 20.479kΩ) 56Ω + 1/19.8470mS

= 118.024  = 41.4394dB

After stage 2 gain established, I decide to recalculate R₆ for standard RIAA gain to get less distortion. (Here -|| means subtract from parallel combination)

AV-stage1-new =

1000 AV-stage2

=

1000 13.3985

= 74.6352(V/V)

R6 =

AV-stage1(Rs + 1/gfs) 4

-||  (R7 || R8 || (rds/4)) =

74.6352(56Ω + 1/19.8470mS) 4

-|| (10MΩ || 442kΩ || 20.479kΩ) =

1.98502kΩ -|| 19.5339kΩ

R6 =

19.5339kΩ x 1.98502kΩ 19.5339kΩ - 1.98502kΩ

= 2.20955kΩ

Would have chosen 2.2kΩ but for slight overgain.  Round down to nearest 1% value:  R₆ = 2kΩ

Stage Two

Calculate r_ds: from LAMBDA and desired 2mA bias

rds =

1 LAMBDA x  iD0

=

1 4.783719m(V-1) x 2mA

=  104.521kΩ

Anticipating V_DS biased at 4V maximum, add contribution of r_ds to effective I_D:

ID = 2mA +

4V 104.521kΩ

=

2.03827mA

Add voltage element for R_s to FET equation by Kirchoff's voltage law and solve for R_s given a desired 2mA bias.
V_G = R_sI_D + V_T + sqrt(I_D/k_n)
R_sI_D =  V_G - V_T - sqrt(I_D/k_n)

Rs =

VG - VT - sqrt(ID/kn) ID

=

2.03179V - -402.5156mV - sqrt(2.03827mA/37.8643mA/V2) 2.03827mA

= 1.08047kΩ

Choose nearest 5% standard value:  R₉ = 1.1kΩ.
This little round to standard value does not merit recalculation of I_D.
Calculate bias limit on R_d:

Rd  <=

VDD - VG - |VT-max| -  vd-peak - (VDRAIN-SAFETY-FACTOR) ID

=

48V - 2.03179V - 2V - 2.82843V - 4V  2.03827mA

= 18.2212kΩ

Calculate g_fs and calculate gain.
g_fs = 2 x sqrt(k_nI_D) = 2 x sqrt(37.8643mA/V² x 2.03827mA) = 17.5702mS
Calculate R_d for desired total gain of 66dB

AV-stage2-target  = 16.82(V/V) =

Rd-total Rs + 1/gfs

=

R11 || rds Rs + 1/gfs

 R_d-total = A_V-stage2(R_s + 1/g_fs) = 16.82(1.1kΩ + 1/17.5702mS) = 19.4593kΩ
Subtract r_ds from parallel R_d-total combination:

R11  =

rds x Rd-total  rds - Rd-total

=

104.521kΩ x 19.4593kΩ 104.521kΩ - 19.4593kΩ

= 23.911kΩ

This value for R₁₁ would violate the bias limit set before, so R₁₁ defaults to bias limited value of 18.2212kΩ
Choose next lower 1% standard value:  R₁₁  = 18.2kΩ
Calculate gain shortfall:

AV-stage2-actual  =

Rd-total Rs + 1/gfs

=

R11 || rds Rs + 1/gfs

=

18.2kΩ || 104.521kΩ (1.1kΩ + 1/17.5702mS)

= 13.3985(V/V)

A_V-LOSS = 13.3985/16.82 = 796.582m
A_V-LOSS-dB = 20log₁₀(796.582m) = -1.97539dB
This is an acceptable design compromise.
SPICE shows distortion more than I would like.
Went  back and recalculated R₆ of stage 1 for overall RIAA standard 40dB of gain at 1kHz to lower distortion.

Calculate input capacitance to prepare to evaluate its affect on RIAA network of previous stage (These formulas are those to calculate reverse-bias diode capacitance which the gate forms with respect to both the drain and the source.):

CGS =

CGS (1 - VGS/PB)0.5

=

CGS (1 - (VT + sqrt(ID/kn))/PB)0.5

CGS =

4.06518e-11 (1 - (-402.5156mV + sqrt(2.03827mA/37.8643mA/V2))/0.981382)0.5

= 37.5228pF

CGD =

CGD (1 - VGD/PB)0.5

=

CGD (1 - (VG - VDD)/PB)0.5

CGD =

3.99e-11 (1 - (2.03179V-(48V - 2.03827mA x 18.2kΩ))/0.981382)0.5

= 12.5923pF

A_V at 2122Hz necessary to calculate Miller capacitance (C_M) is 1/10 of Stage 2 low frequency gain of 13.3985

CG = CGS + CM = CGS + CGD(AV + 1) = 37.5228pF + 12.5923pF(1.33985 + 1) = 66.9869pF

Output Buffer

Figure 4:  LSK170C SPICE model for reference.

.MODEL LSK170C NJF          + BETA   = 0.0278541       VTO    = -0.800434       LAMBDA = 0.0122435          + IS     = 2.45217E-14  + RD     = 12              RS     = 5.8             CGD    = 4.22E-11           + CGS    = 4.23E-11        PB     = 0.9265487 + FC     = 0.5             KF     = 0               AF     = 1

R₁₂ limits short-circuit current through Q₆ to 20mA
R₁₂ >= 48V/20mA = 2.4kΩ.
Choose 5% value:  R₁₂ = 2.4kΩ.
Calculate  V_G .
V_G = V_DD - i_D-Q5R₁₁ = 48V - 2.03827mA x 18.2kΩ = 10.9035V
Min i_DSS of 10mA sets I_D limit.  Choose half at I_D = 5mA.
Calculate r_ds: from LAMBDA and desired 5mA bias

rds =

1 LAMBDA x  iD0

=

1 0.0122435(V-1) x 5mA

=  16.3352kΩ

Given k_n (BETA) = 27.8541mA/V² and V_T = -800.434mV for LSK170C, calculate R_s:

Rs =

VG - VT - sqrt(ID/kn) ID

=

10.9035V - -800.434mV - sqrt(5mA/0.0122435A/V2) 5mA

= 2.21298kΩ

Round up to next 5% value:  R₁₃ = 2.4kΩ.
Output impedance of Q₆ is the inverse of its operating ac transconductance g_fs.
g_fs = 2 x sqrt(k_nI_D) therefore

Rout-Q6 =

1 2 x sqrt(knID)

=

1 2 x sqrt(27.8541mA/V2 x 5mA)

= 42.3682Ω

This value will dominate the output impedance.  Paralleling R₁₃ and R₁₄ with it will only lower it slightly further.
Arbitrarily choose 5% value, R₁₄ = 100kΩ, only to ground output capacitor C₅.

Calculate input capacitance to prepare to evaluate its affect on RIAA network of previous stage:

CGS =

CGS (1 - VGS/PB)0.5

=

CGS (1 - (VT + sqrt(ID/kn))/PB)0.5

CGS =

4.23e-11 (1 - (-800.434mV + sqrt(5mA/27.8541mA/V2))/0.9265487)0.5

= 35.6658pF

CGD =

CGD (1 - VGD/PB)0.5

=

CGD (1 - (VG - VD)/PB)0.5

CGD =

4.22e-11 (1 - (10.9035V - (48V - (5mA x 2.4kΩ)))/0.9265487)0.5

= 7.96283pF

Drain limiting resistor invokes Miller capacitance (C_M) even though it is not in the signal path.  Calculate virtual gain with respect to same and then calculate input capacitance:

AV-buffer  =

Rd-total Rs + 1/gfs

=

R12 || rds Rs + Rout-Q6

=

2.4kΩ || 16.3352kΩ 2.4kΩ + 42.3682Ω

= 856.774m(V/V)

CG = CGS + CM = CGS + CGD(AV + 1) = 35.6658pF + 7.96283pF(856.773m + 1) = 50.451pF

RIAA Analysis

Stage One
Calculate the effective network resistance and solve C₂ for a pole of 75µS.
R_6-network = R₆ || R₇ || R₈ || (r_ds/4) = 2kΩ || 10MΩ || 442kΩ || 20.479kΩ = 1.81425kΩ

C2-network  =

Tpole R6-network

=

75µS 1.81425kΩ

= 41.3395nF

Correct C₂ for input capacitance of next stage:

C2  = C2-network  - CG-stage2 = 41.3395nF - 66.9869pF = 41.2725nF

Stage Two
Calculate the effective DC network resistance and solve for
R_11-network  = R₁₁ || r_ds = 18.2kΩ || 104.521kΩ = 15.5009kΩ
R₁₀ = R₁₁ / 9 = 15.5009kΩ / 9 = 1.72232kΩ

C4  =

Tzero R10

=

318µS 1.72232kΩ

= 184.635nF

Input capacitance of next stage should not affect the 500.2Hz zero formed by C₄ and  R₁₀ but may affect the 50.02Hz pole in a small way only complicated calculations could reveal.  These calculations would be like redoing those of Calculating Passive RIAA Equalization  with input capacitance of the next stage in place of C2 of that circuit interacting with the network at a higher frequency.  I reserve this compensation for the SPICE analysis.

Adjustments

In spite of careful calculations, the RIAA network values will require adjustments during SPICE evaluation due to unexpected and stray effects.  Even then, rounding to standard values will require experimentation to get best frequency response curve. The parts list will show these changes.

SPICE evaluation of unadjusted design circuit was immediately excellent.  The somewhat wavy gain plot sloped down from 20Hz to 20kHz by only 2.25dB.

Figure 5:  Frequency response of unadjusted design circuit

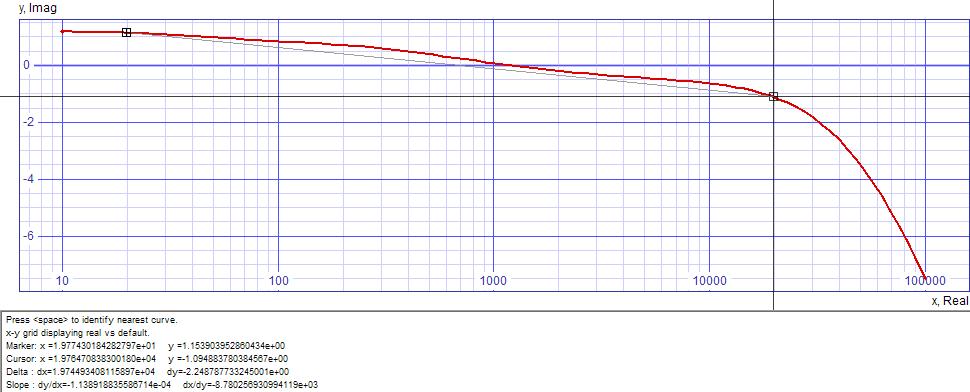SPICE Model, LSK170 SPICE Subckt Models

Optimizing RIAA network values in SPICE rids plot of waviness to slope down from 20Hz to 20kHz by only 1.60dB.  Calculations for adjustments are made in the following linear manner.  If measurement increases with increase in component value, calculate adjustment by:

valuenew =

valuecurrent x

measurementtarget measurementobserved

Else if measurement decreases with increase in component value, calculate adjustment by:

valuenew =

valuecurrent x

measurementobserved measurementtarget

If relationship is strictly linear, you can meet your target with one adjustment calculation.  If not, repeatly recalculate and resimulate until the target is met or close enough for your tolerance criteria.  To help you bend your graph as you desire you should note that frequency plot will slope down at a corresponding pole/zero pair (one in the recorded preequalization and the other in the equalization of your preamp) if any error is on the side of f_pole<f_zero (T_pole>T_zero) and slope up if any error is on the side of f_pole>f_zero (T_pole<T_zero).  You can make your sound bright or warm by your adjustments.

Figure 5:  Frequency response of SPICE optimized circuit

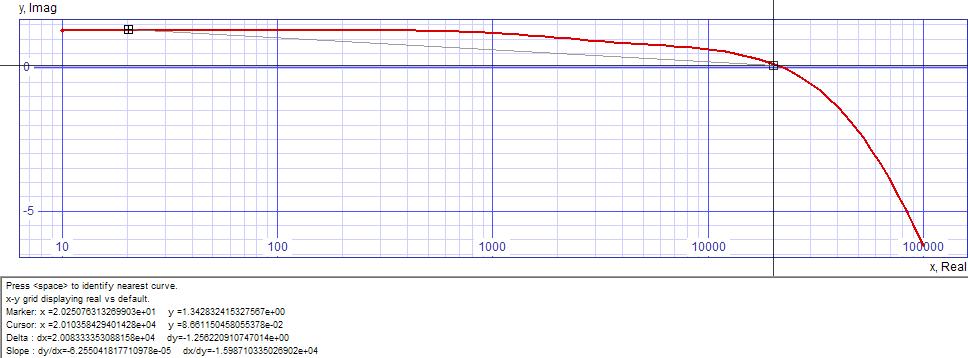SPICE Model, LSK170 SPICE Subckt Models

After careful rounding of component values plot slopes down from 20Hz to 20kHz by only 1.30dB.

Figure 6:  Frequency response of final circuit after choosing standard component values.

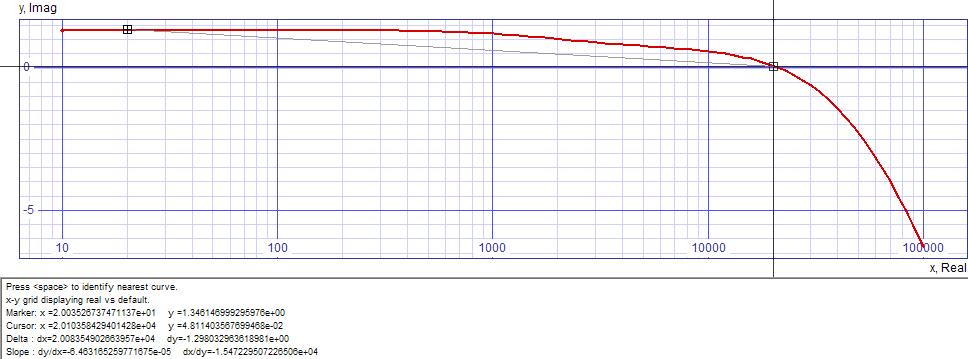SPICE Model, LSK170 SPICE Subckt Models

Higher than anticipated JFET transconductance may require raising supply voltage to prevent drain saturation.  Unexpected distortion of prototype may be aleviated by raising power supply voltage.

Other SPICE Findings

SNR = 102.98dB relative to 1V_rms output.  This would be relative to a 10mV cartridge output amplified by 40dB gain at 1kHz.  SNR will vary with cartridge output after you compensate with your volume control.

Fourier analysis for vout: (Distortion performance at 7.071mV_peak(5mV_rms) and 1kHz and breakdown by harmonic)
Fourier analysis for vout:
No. Harmonics: 10, THD: 0.0178052 %, Gridsize: 200, Interpolation Degree: 1

Harmonic	Frequency	Magnitude	Phase	Norm. Mag	Norm. Phase
--------	---------	---------	-----	---------	-----------
0	0	0	0	0	0
1	1000	0.879288	-92.635	1	0
2	2000	0.000146834	-19.801	0.000166992	72.8345
3	3000	5.41796e-005	-38.326	6.16175e-005	54.3094
4	4000	3.23322e-006	-95.464	3.67709e-006	-2.8289
5	5000	1.56558e-006	-131.85	1.78051e-006	-39.21
6	6000	3.12765e-007	-88.13	3.55703e-007	4.50502
7	7000	1.21373e-006	-45.309	1.38036e-006	47.3267
8	8000	2.42554e-007	-80.335	2.75853e-007	12.3003
9	9000	7.75152e-007	58.3996	8.81568e-007	151.035

Fourier analysis for vout: (Distortion performance at 100Hz and proportionate level to 1kHz and breakdown by harmonic)
  No. Harmonics: 10, THD: 0.0190292 %, Gridsize: 200, Interpolation Degree: 1

Harmonic	Frequency	Magnitude	Phase	Norm. Mag	Norm. Phase
--------	---------	---------	-----	---------	-----------
0	0	0	0	0	0
1	100	0.891848	-90.243	1	0
2	200	0.000169612	170.701	0.00019018	260.944
3	300	5.79251e-006	-75.974	6.49495e-006	14.2693
4	400	3.3312e-007	49.7897	3.73516e-007	140.033
5	500	2.1084e-007	94.8152	2.36408e-007	185.058
6	600	1.69153e-007	96.0689	1.89666e-007	186.312
7	700	1.44333e-007	96.9693	1.61835e-007	187.212
8	800	1.2705e-007	97.6061	1.42457e-007	187.849
9	900	1.13432e-007	98.8471	1.27188e-007	189.09

Fourier analysis for vout:  (Distortion performance at 10kHz and proportionate level to 1kHz and breakdown by harmonic)
  No. Harmonics: 10, THD: 0.345553 %, Gridsize: 200, Interpolation Degree: 1

Harmonic	Frequency	Magnitude	Phase	Norm.Mag	Norm.Phase
--------	---------	---------	-----	---------	-----------
0	0	0	0	0	0
1	10000	0.821345	-102.31	1	0
2	20000	0.00283777	-107.17	0.00345502	-4.8656
3	30000	4.86413e-005	-79.038	5.92215e-005	23.2697
4	40000	2.79079e-006	168.487	3.39783e-006	270.794
5	50000	9.02139e-007	-74.142	1.09837e-006	28.1659
6	60000	9.62636e-007	-84.247	1.17202e-006	18.0606
7	70000	8.13981e-007	-83.821	9.91034e-007	18.4866
8	80000	7.11331e-007	-82.815	8.66056e-007	19.4925
9	90000	6.33031e-007	-81.892	7.70725e-007	20.4162

Miscellaneous Calculations

Now set coupling capacitor values C₃ and C₅ for best bass response:
Initially desire both highpass poles at 0.1Hz for nearly no affect at 20Hz.

R_pole = R₆ || (r_ds/4) + R₇ || R₈ = 2kΩ || 20.479kΩ + 10MΩ || 442kΩ = 1.82206kΩ + 423.291kΩ = 425.113kΩ

C3 =

1 2πfpoleRpole

=

1 2π x 0.1Hz x 425.113kΩ

= 3.74383µF

Round up to next 20% standard value.  Choose C₃ = 3.9µF polyethylene.

Assuming a high impedance load (R_L >= 10kΩ):
R_pole = R_out-Q6  + R₁₄ || R_L = 42.3682Ω + 100kΩ || 10kΩ = 9.13328kΩ

C5 =

1 2πfpoleRpole

=

1 2π x 0.1Hz x 9.13328kΩ

= 174.258µF

Round up to next 10% standard value.  Choose C₅ = 180µF electrolytic
If you want a polyethylene capacitor here choose C₅ = 10µF and recalculate pole:

fpole =

1 2πC5Rpole

=

1 2π x 10µF x 9.13328kΩ

= 1.74258Hz

Highpass response is only down -0.033dB at 20Hz with this choice of 0.1Hz and 1.74258Hz poles.

You may recalculate C₅ if you want to drive 600Ω.

Calculate load current from power supplies V_DD1, V_DD2, and V_DD3.
i_DD1 = i_Q1-BIAS x 4 + i_R7-R8 = 2.551918mA x 4 + 48V/(10MΩ + 442kΩ)  = 10.2123mA
i_DD2 = i_Q6-BIAS = 2.03827mA
i_DD3 = i_Q6-BIAS = 5mA

Design Decisions Left to You

• R₁ and C₁ should be calculated per article Phono Termination Calculations and Calculator.
• This circuit and its analysis is only given as a design example; change everything if you like.
• A low noise 48V power supply.  The Line Level Class A Power Supply  presented earlier will require a design improvement to deliver 48V.  The LM317 used as a preregulator has a 40V limit on the input/output differential.  See the LM317 datasheet for ideas.
• Whether protection zeners (39V) should be used to protect from drain overvoltage.  (Connected from drain to source or ground.)  Load resistors may provide sufficient protection.
• Resistor wattage given for normal operation.  Decide whether more wattage is needed at power up.
  
• In spite of careful design, transistor parameter variations may require more adjustments during the prototyping process.  The specifications in this design are only valid if the JFETs match the SPICE model parameters.  ;=(
  

Document History
June 26, 2010  Created
July 3, 2010  Recalculated with 48V power supply and RIAA standard gain.
January 26, 2011  Removed personal comment at beginning.  Made minor symbol improvements.
March 26, 2011  Corrected numerical typo at end of first stage calculations not affecting their results and a misspelling in the SPICE results.