Home  │ Audio Home Page

Copyright © 2012 by Wayne Stegall
Updated July 8, 2012.  See Document History at end for details.

Floating Source-follower Regulator

Introduction

At the moment that I realized that the inner feedback loop added to the amplifier for its desirable attributes connected ripple from the VDD1 supply line into open-loop signal path, it became necessary to regulate the offending voltage.  I already held this regulator in my mind as one for non-feedback circuits to get the maximum voltage out that the properties of the regulating MOSFET would allow.

Regulator Design

The operation of the regulator in figure 1 below is based on a MOSFET being in current amplification mode if the following condition is met.

(1)	VDS > VGS - VT.

With V_DS ≈ V_GS, regulation is possible if negative ripple deviation does not exceed ≈2V_T.

R1 and C1 filter ripple to a level low enough to be eliminated by the diode filter comprised of the parallel diodes and C3.  V_G then takes the average of the ripple peaks and dips in V_D.  Assuming V_G is filtered to a constant value:

(2)	VDS =  VGS ± ½vpeak-ripple

Take the ripple dip as worst case

(3)	VDS =  VGS - ½vpeak-ripple

Combine equations 1 and 3 to get:

(4)	VGS - VT <  VGS - ½vpeak-ripple

Solve to get design equation

(5)	vpeak-ripple  < 2VT.

Figure 1:  Floating source-follower regulator

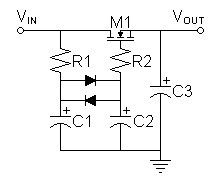Design Methodology

• Calculate capacitance in preceding raw supply to give ripple less than 2V_T of regulating MOSFET.
• Calculate R1 for balance between low noise and reasonable current limits.
• Calculate C1 for a RC constant giving ripple low enough at input to diode filter to allow diode impedance high enough to eliminate the remaining ripple.  Initially 25mV seems a good target because it is a figure of merit in the real diode equation.
  
• Arbitrarily choose C2 to give high RC constant appropriate for expected high Z of parallel diodes, then adjust if necessary during simulation.
• Choose R2 as normal to prevent LC oscillations in regulating MOSFET.
• Calculate C3 to give desired suppression of nonlinearity of regulating MOSFET.

If you want more regulation for peak ripple exceeding two diode drops (≈1.3-1.4V) a clamping diode can be added in parallel with R1 as in figure 2 below.  Then V_G will ride at one diode drop above the ripple minimum rather than at the higher ripple average.

Figure 2:  Floating source-follower regulator clamped to ripple minimum

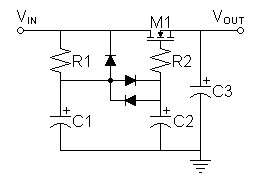The only change in design methodology is the added difficulty in calculating R1 and C1 for ripple reduction to desired small level to drive the diode filter.  Initially, I would estimate the ripple at the junction of R1 and C1 to double due to C1 only seeing half of R1 due to the parallel diode.  Doubling R1 or C1 might be sufficient.

Power Supply Design

Figure 3:  Floating source follower regulators added to One-Bend Amplifier power supply

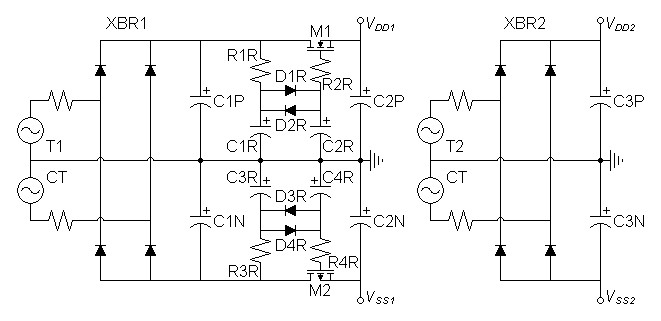SPICE shows I_VDD1 = 169mA and I_VSS1 = 182mA, assume both could vary with a maximum of 200mA.  Design to 1V ripple at regulator input.

(6)

C1P =

i fΔv

=

200mA 120Hz × 1V

= 1.66667mF

Round up to nearest 20% standard value:  C1P and C1N = 2.2mF
If the raw V_DD1 and V_SS1 supply are used to supply the regulators for two channels double the value and round up to 4.7mF.

If R1R is chosen to be 1kΩ, calculate C1R to reduce ripple seen at input of diode filter to 25mV.

(7)

fRC = fripple ×

vfiltered-ripple vripple

= 120Hz ×

25mV 1V

= 3Hz

(8)

C1R =

1 2πfR

=

1 2π × 3Hz × 1kΩ

= 106.103µF

Round up to nearest 20% standard value:  C1R = 150µF

From datasheet and SPICE model, I estimate the impedance of the filter diodes with a signal of 25mV to be >196MΩ.  Since their operating resistance of filter is so high  choose C2R arbitrarily.
C2R = 10µF

Choose gate resistor
R2R = 100Ω

I used the TF analysis of SPICE to get output impedance representing that of M1 and M2 without effect of C2P and C2N..
Z_VDD1 = 2.68632Ω
Z_VSS1 = 1.7812Ω

If C2P and C2N are desired to bypass the transfer curves of the regulators M1 and M2, I thought to calculate their values for a pole of 20Hz or lower assuming that the feedback factor in the amplifier will reduce if further at that frequency.  Use worst case of Z_VSS1.

(9)

C2N =

1 2πfR

=

1 2π × 20Hz × 1.7812Ω

= 4.46762mF

Round up to nearest 20% standard value:  C2P and C2N = 4.7mF

Initially transformer T2 was chosen at 48VCT to meet the power specifications.  Since the new design goal was to reduce hum the second transformer could not ride the first piggyback and was separated.  Then the value of T1 was raised to 70VCT after the regulators were verified to allow predrivers to drive output MOSFETs to clipping to as close to V_DD2 and V_SS2 as possible.

To measure the hum this circuit was designed to reduce do a transient and Fourier analysis at 120Hz and calculate total.

Fourier analysis for vdd1:
  No. Harmonics: 10, THD: 71.5238 %, Gridsize: 200, Interpolation Degree: 1

Harmonic	Frequency	Magnitude		Phase		Norm. Mag		Norm. Phase
0	0	0		0		0		0
1	120	9.78238e-006		90.3868		1		0
2	240	4.70278e-006		92.1464		0.48074		1.75963
3	360	3.24187e-006		92.5358		0.331399		2.14902
4	480	2.36656e-006		93.605		0.241921		3.21826
5	600	1.93237e-006		94.4977		0.197536		4.11092
6	720	1.58949e-006		95.3495		0.162485		4.96269
7	840	1.37518e-006		96.3245		0.140578		5.93777
8	960	1.19909e-006		97.158		0.122577		6.77119
9	1080	1.06692e-006		98.1152		0.109065		7.72844

Calculate total hum voltage from Fourier data.

(10)

vhum-total = vhum-120Hz × (1 + THD) = 9.78238µV ×

1 +

71.5238% 100%

= 16.7791µV

Calculate decibel hum relative to 1W level (2.82843V into 8Ω) for relevance to speaker sensitivity

(11)

dBhum = 20 × log

16.7791µV 2.82843V

= -104.536dB

The calculation for the hum on V_SS1 produces nearly identical results. 

SPICE Model of standalone power supply setup for hum analysis.

The astute reader might ask why hum had been reduced only modestly after talking about the diode filter eliminating hum.  This expectation only applies to the voltage applied to the gate of the MOSFET.  The hum that results is a factor of an ac drain to source leakage resistance (r_ds) in the hundreds of kΩ limiting the ability of the MOSFET to completely eliminate the hum in a non-feedback regulator.

Amplifier Calculations and Simulation Based on New Power Supply

Figure 4:  One-Bend Amplifier of part 3 used to evaluate new power supply.

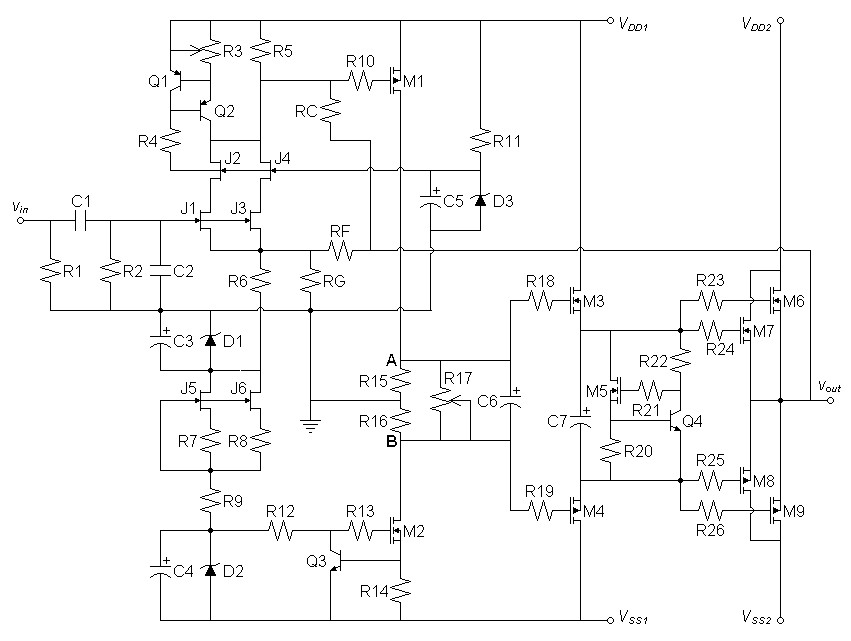Fourier analysis for vout:
  No. Harmonics: 16, THD: 73.9737 %, Gridsize: 200, Interpolation Degree: 3

Harmonic	Frequency	Magnitude		Phase		Norm. Mag		Norm. Phase
0	0	0		0		0		0
1	120	7.35694e-007		-90.352		1		0
2	240	3.50513e-007		-86.723		0.476439		3.62866
3	360	2.45267e-007		-88.138		0.333382		2.21388
4	480	1.77279e-007		-86.203		0.240968		4.14873
5	600	1.44661e-007		-85.272		0.196632		5.08042
6	720	1.1996e-007		-84.859		0.163057		5.49244
7	840	1.03007e-007		-83.545		0.140014		6.80699
8	960	8.98178e-008		-82.893		0.122086		7.45894
9	1080	8.02879e-008		-81.829		0.109132		8.52283
10	1200	7.23776e-008		-80.99		0.0983799		9.36166
11	1320	6.53764e-008		-80.166		0.0888635		10.1863
12	1440	6.05716e-008		-79.155		0.0823326		11.1972
13	1560	5.54925e-008		-78.23		0.0754288		12.1215
14	1680	5.18678e-008		-77.512		0.0705019		12.8395
15	1800	4.83759e-008		-76.464		0.0657555		13.8882

Calculate total hum voltage from Fourier data.

(12)

vhum-total = vhum-120Hz × (1 + THD) = 735.694nV ×

1 +

73.9737% 100%

= 1.27991µV

Calculate decibel hum relative to 1W level (2.82843V into 8Ω) for relevance to speaker sensitivity

(13)

dBhum = 20 × log

1.27991µV 2.82843V

= -126.887dB

This value of hum will not be heard with speakers of any known sensitivity.

A quick look at other SPICE results suggest amplifier performing substantially as in third article except for hum improvement.

SPICE model of amplifier
SPICE model of power supply setup to include in the amplifier model

Recommended Amplifier Improvement

I recommend that an actual prototype of the amplifier add a coupling capacitor in series with inner feedback resistor R_C to give a subsonic zero.  This will improve DC offset at the output in two ways:

• By reducing offset drift with power supply voltage variation.
• By removing DC from inner feedback loop, full DC gain works with global feedback for greatest reduction in DC offset.

I left this capacitor out of the prior simulations because it wrecked the transfer curve analysis as the DC transfer analysis removes capacitors from the circuit and therefore the entire effect of having an inner feedback loop.

For R_C of 100kHz and a highpass zero of 1Hz this capacitor calculates:

(14)

CIFB =

1 2πfR

=

1 2π × 1Hz × 100kΩ

= 1.59155µF

Round up to nearest 20% standard value:  C_IFB = 2.2µF

Links

Previous articles in this series:

• One-Bend Amplifier  January 31, 2012.  Part 1:  Compare a current-feedback amplifier allowing a one-bend distortion characteristic to its voltage-feedback equivalent.  Updated  March 14, 2012  Added correction concerning output stage transconductance factor and added a link to the next article.
• One-Bend Amplifier  March 14, 2012.  Part 2:  Improving important details of a current-feedback amplifier.
• One-Bend Amplifier  June 6, 2012.  Part 3:  Modified circuit adds a predriver stage.

Document History
July 7, 2012  Created.
July 7, 2012  Corrected wrong value after equation 14 and added some additional text.
July 8, 2012  Added comment about the MOSFET's limited hum suppression capability after equation 11.