Cascode Phono Preamplifiers

SPICE verified. Capacitively coupled cascode enables an easily adjustable single-stage preamp.

Introduction

Investigation of a preamp illustrating a low-noise application of the inverting RIAA equalization circuit lead to this discrete preamp design. Although it appears to be a two stage circuit with a buffer, the second stage is only a cascode to the first stage, creating a virtual one-stage design. Separating the class-a input from the cascode with a capacitor enables separate biasing for each. Thus the cascode can have a lower current bias than the input enabling the necessary gain from one stage without excessively high voltage supplies. A direct cascode design would require a power supply in excess of 200V. I investigated two variations on the circuit that did not produce results as good as this one. One was a direct cascode with a shunt resistor around the cascode to the positive supply to reduce cascode bias, resulting in higher distortion. The other was a direct cascode with a shunt current source around the cascode to the positive supply to reduce cascode bias, resulting in lower distortion with higher noise. Both of these had more sensitive and difficult to adjust bias issues. This one turned out simpler in the end.

Discrete Circuit

Figure 1: Schematic of Passive Cascode Phono Preamplifier

Parts List
R_i¹	47kΩ	C_1N-B⁴	2.2nF 1%
C_i¹	25pF	R_2N	2.61kΩ 1%
Q₁-Q₈	LSK170A n-channel jfet	C_2N-A⁴	39nF 1%
R₁-R₈	27.4Ω	C_2N-B⁴	3.3nF 1%
R₉²	750Ω 5%	Q₁₀,Q₁₁	LSK170C n-channel jfet
C₁	2200µF electrolytic	R₁₁	75Ω 5%
Q₉	2N3904 small signal NPN³	C₂	100µF electrolytic
R₁₀	13kΩ 5%	R₁₂	1kΩ 5%
R_1N	18.2kΩ 1%	R₁₃	100kΩ 5%
C_1N-A⁴	120nF 1%

Notes:
¹Values calculated for your cartidge can be substituted for default values shown.
²The actual hardware circuit may require hand choosing R₉ for the correct V_D bias due to JFET parameter variations.
³SPICE simulation showed no significant noise improvement by upgrading to an ultralow noise BJT (i.e. MAT02) because gain falls entirely to input stage.
⁴A-B capacitor pairs are connected together in parallel.

Initial Design Decisions

Choose +30V supplies for VDD and VCC. choose -15V supply for VEE.
Want gain of 46dB at 1kHz to amplify 5mV to 1V_rms.

Design

Transconductance Front-end Design

It is desirable to choose source resistors small enough to make their noise contribution insignificant compared to the JFET to lower noise.

(1)

Resistor noise equation (per √Hz, figure of merit, does not account for bandwidth)

v_{n-resistor-rtHz} =

4kTR

Rearrange resistor noise equation to calculate equivalent input noise resistance of JFET.

(2)

R =

v_{n-resistor-rtHz}²

4kT

1nV²

4 x 1.3806504e-23 x 298.15ºK

= 60.7325Ω

Choose 27Ω source resistors on the chance that lower values will be acceptable. This presumes averaging among eight parallel devices will greatly stablize average transistor parameters. Choose nearest 1% value to allow use of metal-film resistors.
R₁-R₈ = 27.4Ω

Figure 2: LSK170A SPICE model for reference

.MODEL LSK170A NJF
+ BETA   = 0.0378643       VTO    = -0.4025156      LAMBDA = 4.783719E-3
+ IS     = 3.55773E-14
+ RD     = 10.6565         RS     = 6.8790487
+ CGD    = 3.99E-11        CGS    = 4.06518E-11
+ PB     = 0.981382        FC     = 0.5
+ KF     = 0               AF     = 1

It is possible to calculate a gate voltage bias from a drain current specification, but iteration (repetitive computer calculations) or a load line graph are required to calculate the current bias from a specified gate voltage bias. To begin small signal analysis from the parameters given (V_GS = 0V and R_S = 27.4Ω), get current bias from preliminary SPICE deck.

SPICE shows a combined drain current of 26.3811mA. Individual drain current then calculates to 3.29764mA.

Calculate JFET transconductance:

(3)

g_fs = 2 ×

k_nI_D

= 2 ×

37.8643mA/V² x 3.29764mA

= 22.3484mS

Calculate transconductance of individual parallel elements then of entire circuit front-end:

(4)

g_{fs-ckt-element} =

R_S + 1/g_fs

27.4Ω + 1/22.3484mS

= 13.8608mS

(5)	g_fs-front-end = 8 × 13.8608mS = 110.886mS

Because this stage will drive a cascode through C₁, there will be only a trace of AC at V_D and therefore no headroom requirement. Because higher values of R₉ and R₁₀ will lower distortion as regards the ac impedance seen by the emitter of Q₉, choose V_D bias at 10V to maximize R₉, and calculate R₉.

(6)

R₉ =

V_{DD -}V_D

I_D-TOTAL

30V - 10V

26.3811mA

= 758.119Ω

Round to nearest 5% value:
R₉ = 750Ω

Calculate C₁ for a pole of 0.1Hz

(7)

C₂ =

2π × R₉ × f_hp

2π × 750Ω × 0.1Hz

= 2.12207mF

Round up to nearest 20% value:
C₂ = 2200µF

Cascode Design

Calculate DC gain for the desired 46dB gain at 1kHz.

(8)	A_V-DC = 9.89808 × A_V-1kHz = 9.89808 × 200V/V = 1979.62V/V

Given A_V-DC = g_fs-front-end × R_1N calculate R_1N for chosen gain.

(9)

R_1N =

A_V-DC

g_fs-front-end

1979.62V/V

110.886mS

= 17.8527kΩ

Reserve final choice of R_1N for adjustments below.

R₁₀ has two effects on distortion: As pertains to bias, lowering R₁₀ will lower distortion by increasing the bias. As pertains to ac impedance, the parallel of R₉ and R₁₀ lower distortion as they are raised. Because R₉ is much lower than the expected R₁₀, prefer to choose R₁₀ to increase bias relative to other factors. Choose V_C bias at 10V as a compromise between a low R₁₀ and reasonable headroom, and calculate R₁₀.

(10)

R₁₀ =

R_1N × V_R10

V_R1N

17.8527kΩ(-0.7V - -15V)

(30V - 10V)

= 12.7647kΩ

Round to nearest 5% value:
R₁₀ = 13kΩ

Output Buffer Design

The choice of JFET in the output buffer stage is not critical. As for noise the gain stages have amplified their noise enough to make that of the output less critical. Consider that 1nV/√Hz amplified by about 100 gain at 1kHz is 100nV/√Hz. A common 2N3819 would be a good choice as would others in this respect. It is better to prioritize the maximization of g_fs in order to reduce buffer stage distortion. To this end, an LSK170 would be a best known choice due to high k_n and g_fs, with the lowest possible noise for a bonus. Since you would be faced with component variations on a part of your own choice, I suggest you choose a value of R₁₁ by trial and error to get a bias current within your JFETs specifications. You should not match Q₁₀ and Q₁₁. Rather, because Q₁₀ will operate freer if it is not pushed to its current limit, you should choose Q₁₀ to have a higher g_fs than Q₁₁. To this end, try both transistors in the Q₁₁ position and place the one there that gives the lowest bias current through Q₁₁. Since this aspect is experimental, calculating R₁₁ may be overengineering. A R₁₁ corresponding to the JFET's rated g_fs would be a good starting point for a midpoint bias, i.e.:

(11)

R₁₁ =

g_fs

10mS

= 50Ω

or alternatively setting R_S to ratio of cutoff voltage to maximum current for another approximate midpoint bias:

(12)

R₁₁ =

|V_T|

|I_DSS|

20mA

= 100Ω

If you must make an exact calculation from a chosen I_D, the following was derived from the FET equation by circuit analysis:

(13)

R_S =

V_T - sqrt(I_D/k_n)

I_D

Choose R₁₁ = 75Ω as median of two estimates.

Choose R12 output limiter for worst case of 10mA maximum gate current and 20mA maximum drain current.

(14)

R₁₂ =

VCC

I_S-MAX

30V

30mA

= 1kΩ

Calculate output coupling capacitor to give 1Hz highpass pole with a 600Ω load knowing that the pole frequency will be much lower with a more reasonable load of 10kΩ:

(15)

C₂ =

2π × R_L-MIN × f_hp

2π × (1kΩ + 600Ω) × 1Hz

= 99.4718µF

Round up to next standard value C₃ = 100µF

RIAA Analysis

Because the preliminary SPICE deck produced excellent frequency response, I left stray impedances out of the calculations.
These calculations are carried out according to the document Phono Equalization Calculations: Passive RIAA Network.

Given R_1N = 17.8527kΩ, Calculate R_2N.

(16)

R_2N =

R_1N

6.877358491

17.8527kΩ

6.877358491

= 2.59587kΩ

Calculate C_1N and C_2N from R_1N.

(17)

C_1N =

2187µs

R_1N

2187µs

17.8527kΩ

= 122.502nF

(18)

C_2N =

750µs

R_1N

750µs

17.8527kΩ

= 42.0105nF

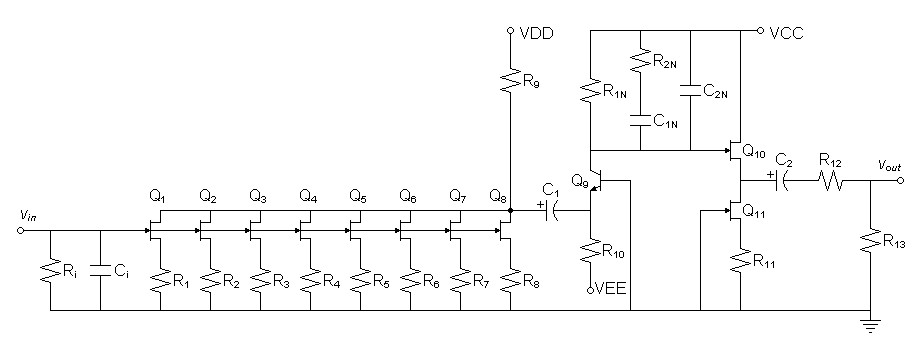
These equalization calculations produce the following plot in SPICE where the response is down to -0.578dB at 20kHz after a 0.07dB rise in the midrange.

Figure 3: SPICE Bode Plot of Discrete Circuit with Initial Values

SPICE deck for discrete circuit with inital values.
Supporting models: lsk170.txt, models1.txt, mat02_03.txt, invriaa2.txt.

Adjustments to Discrete Circuit

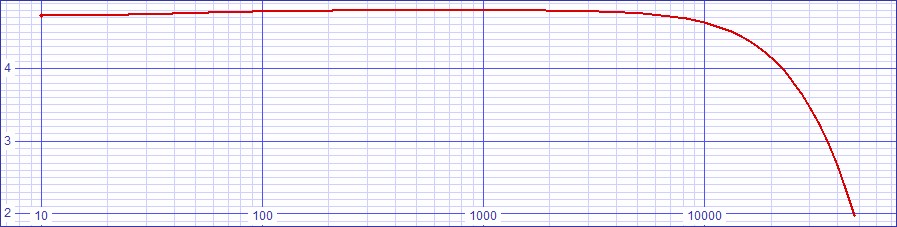
Standard value component choices produce the following plot where the response trends generally down to -0.784dB at 20kHz. The standard values producing this response are logged in the parts list above.

Figure 4: SPICE Bode Plot of Discrete Circuit after Standard Value Choices

The actual hardware circuit may require hand choosing R₉ for the correct V_D bias due to JFET parameter variations. The bias on the cascode will not require adjustment because BJT voltage bias is accurately predictable.

SPICE deck for discrete circuit with standard value choices.
Supporting models: lsk170.txt, models1.txt, mat02_03.txt, invriaa2.txt.

Other Spice Results

S/N ratio is 104.415dB relative to 1V_RMS output.
Add 4.71685dB for gain over RIAA for normalized S/N of 109.13185dB

Fourier analysis for vout is dominated by second harmonic:
No. Harmonics: 16, THD: 0.552496 %, Gridsize: 1024, Interpolation Degree: 3

Harmonic	Frequency	Magnitude	Norm.Mag	Percent	Decibels

1	1000	1.24009	1	100	0
2	2000	0.00656276	0.00529215	0.529215	-45.52735709
3	3000	0.00151543	0.00122202	0.122202	-58.25843372
4	4000	0.00079421	0.000640444	0.0640444	-63.87037677
5	5000	0.000486011	0.000391915	0.0391915	-68.13616228
6	6000	0.00040426	0.000325991	0.0325991	-69.7358878
7	7000	0.00035357	0.000285115	0.0285115	-70.89959867
8	8000	0.000310044	0.000250016	0.0250016	-72.04064395
9	9000	0.000275186	0.000221908	0.0221908	-73.07654081
10	10000	0.000247239	0.000199371	0.0199371	-74.00676026
11	11000	0.000225024	0.000181457	0.0181457	-74.82452547
12	12000	0.000206485	0.000166508	0.0166508	-75.57129791
13	13000	0.000190323	0.000153475	0.0153475	-76.27924716
14	14000	0.000176728	0.000142512	0.0142512	-76.9229713
15	15000	0.000165178	0.000133198	0.0133198	-77.51004592

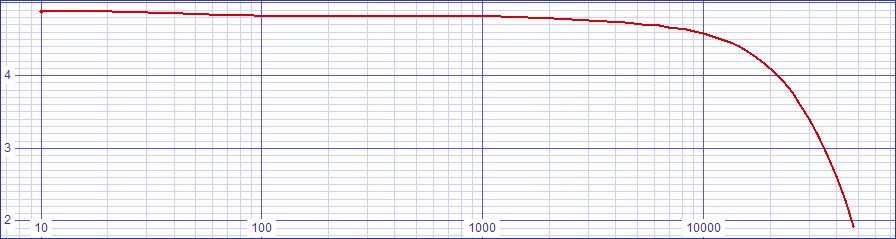
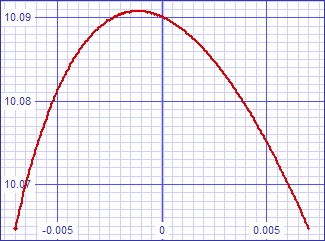
I expect that gain change with frequency will change the way preequalization and postequalization transfer curves juxtapose to create the final transfer curve. Therefore transfer error curve analysis is given for three frequency ranges:

Figure x: Transfer curve error at DC-50Hz	Figure x: Transfer curve error at 1kHz	Figure x: Transfer curve error at 21kHz

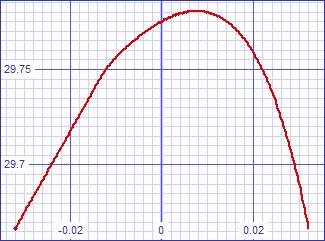I initally attributed an incorrect cause to the fact that all of these curves have a bend direction opposite that of the hybrid circuit because I falsely presumed the hybrid circuit to be inverting as the discrete one. Now I attribute it to this discrepancy.

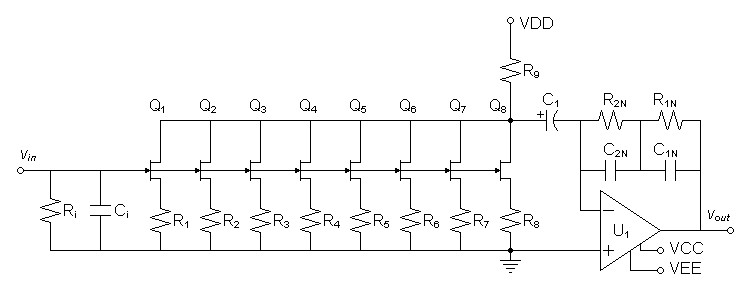
Hybrid Circuit

Figure 5: Schematic of Hybrid Cascode Phono Preamplifier

Parts List
R_i¹	47kΩ	R_1N	16.5kΩ 1%
C_i¹	25pF	C_1N-A³	180nF 1%
Q₁-Q₈	LSK170A n-channel jfet	C_1N-B³	13nF 1%
R₁-R₈	27.4Ω	R_2N	1.4kΩ 1%
R₉²	750Ω 5%	C_2N-A³	51nF 1%
C₁	2200µF electrolytic	C_2N-B³	2.7nF 1%
U₁	OPA227 operational amplifier

This is the circuit that inspired the one above.

Initial Design Decisions

Choose +30V supply for VDD, +15V supply for VCC, and -15V supply for VEE.
Want gain of 46dB at 1kHz to amplify 5mV to 1V_rms.

Transconductance Front-end Design

This circuit has the same front-end design as the discrete version. It is only necessary to carry forward the resistance calculated for R_1N in the discrete circuit as the DC impedance of the inverting RIAA network used here and do the RIAA Analysis.

RIAA Analysis

These calculations are carried out according to the document Phono Equalization Calculations: Inverting RIAA Network.

Given R_1N + R_2N = 17.8527kΩ, Calculate R_1N and R_2N.

(19)

R_1N =

17.8527kΩ × 11.7778

12.7778

= 16.4556kΩ

(20)

R_2N =

17.8527kΩ × 1

12.7778

= 1.39717kΩ

(21)

C_1N =

T_P1

R_1N

3180µs

16.4556kΩ

= 193.247nF

(22)

C_2N =

T_P2

R_2N

75µs

1.39717kΩ

= 53.6799nF

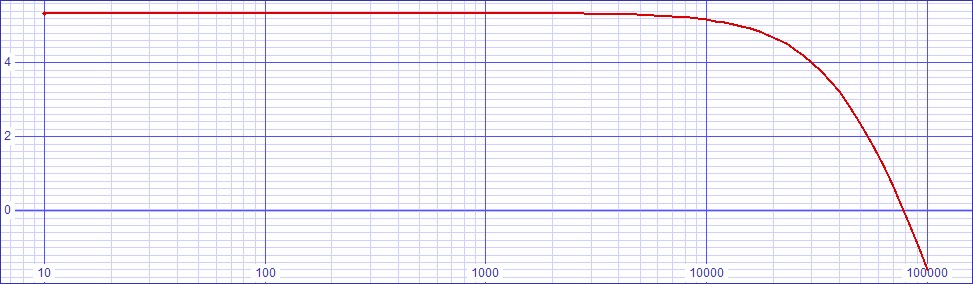
These equalization calculations produce the following plot in SPICE where the response is flat until down to -0.637dB at 20kHz

Figure 6: SPICE Bode Plot of Hybrid Circuit with Initial Values

SPICE deck for hybrid circuit with inital values.
Supporting models: lsk170.txt, OPA227.txt, AD797AN.txt, invriaa2.txt.

Adjustments to Hybrid Circuit

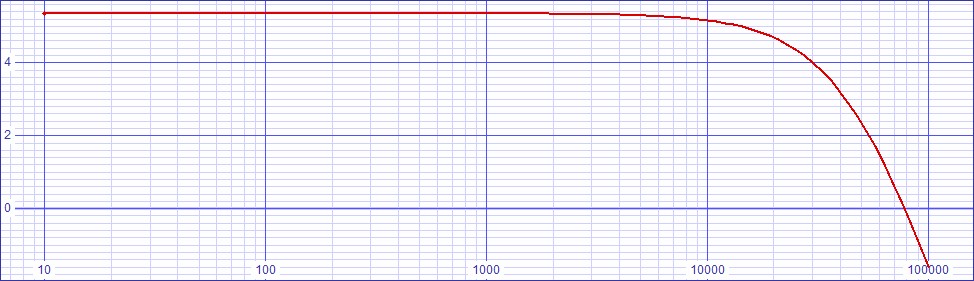
Because this circuit places its operational amplifier after first-stage transconductance gain, it seemed that it would not require an ultralow-noise operational amplifier such as an AD797 or a NME49990. After simulating SPICE an AD797 with an ultralow noise spec of 0.9nV/√Hz as a baseline, I first tried an AD825 with an ordinary noise spec of 12nV/√Hz as an alternative because of its 10kHz dominant pole. This combination lost the circuit 1dB of SNR compared to the AD797. I then tried an OPA227 with a low noise spec of 3nV/√Hz as a compromise. Because it simulated essentially the same noise results as the AD797, I chose it as a more cost effective alternative.

Standard value component choices produce the following plot where the response is flat until down to -0.657dB at 20kHz. The standard values producing this response are logged in the parts list above.

Figure 6: SPICE Bode Plot of Hybrid Circuit after Standard Value Choices

SPICE deck for hybrid circuit with standard value choices.
Supporting models: lsk170.txt, OPA227.txt, AD797AN.txt, invriaa2.txt.

Other Spice Results

S/N ratio is 1.03896dB relative to 1V_RMS output.
Add 5.1915dB for gain over RIAA for normalized S/N of 109.088dB

Fourier analysis for vout:
No. Harmonics: 16, THD: 0.148538 %, Gridsize: 1024, Interpolation Degree: 3

Harmonic	Frequency	Magnitude	Norm.Mag	Percent	Decibels

1	1000	1.30842	1	100	0
2	2000	0.00100123	0.000765218	0.0765218	-62.32429645
3	3000	0.000961284	0.00073469	0.073469	-62.67791743
4	4000	0.000729173	0.000557292	0.0557292	-65.07834383
5	5000	0.000576157	0.000440345	0.0440345	-67.12413861
6	6000	0.000485056	0.000370719	0.0370719	-68.6191031
7	7000	0.000413432	0.000315978	0.0315978	-70.00686308
8	8000	0.000363602	0.000277894	0.0277894	-71.1224166
9	9000	0.000322851	0.000246748	0.0246748	-72.15492718
10	10000	0.000291564	0.000222837	0.0222837	-73.04025394
11	11000	0.000264078	0.00020183	0.020183	-73.9002856
12	12000	0.00024286	0.000185613	0.0185613	-74.6278322
13	13000	0.000223275	0.000170645	0.0170645	-75.35812865
14	14000	0.000207823	0.000158835	0.0158835	-75.98107585
15	15000	0.000194001	0.000148271	0.0148271	-76.57887567

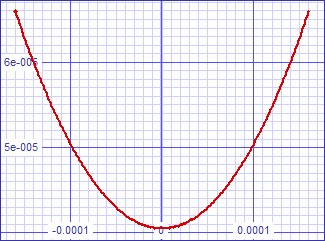
For now I presume that preequalization transfer curve of the JFET front end dominates due to the seemingly vanishing distortion specification of the operational amplifier. Therefore I expect that the low frequency transfer error curve will suffice for the entire audio band:

Figure x: Transfer curve error at DC-50Hz

Document History
May 3, 2011 Created.
May 4, 2011 Added missing × symbol in equation (5), reformatted equation (1), update figure 5 schematic and revised explanation of R₁₀ choice preceding equation (10).
May 6, 2011 Completed hybrid design promised for second circuit.
May 6, 2011 Updated SPICE decks to replace any unchanged preliminary values with correct calculated ones. The differences were not ones expected to change the results.
May 10, 2011 Corrected two grammar and spelling faults.
May 20, 2011 Improved SPICE decks to reduce interpolation noise in fourier results.
March 3, 2012 Added transfer error curve analysis for both circuits. Corrected incorrect interpretation of inverted transfer error curve bend direction between circuits.