Straight Intonation

Calculate the approximate intonation error of an intonation with a straight nut and saddle.

Introduction

If the intonation correction at the nut and saddle is different for every string on a guitar, then the straight nut and saddle of most guitar setups are a compromise. I thought it might be interesting to estimate how much error is present in these setups and whether it is reasonably audible. The custom compensation is assumed perfect then each alternative intonation is calculated for error in mm and then in cents. Cents are an exponential percentage calculation tailored to representing frequency error. 100 cents = 1 semitone. The reader is then to infer an approximately linear and/or inversely-linear relationship between changes in string length and the associated frequencies.

As a point of reference it may be reasonable to think the error introduced by equal-temperament tuning relative to perfect harmonic tuning (just temperament) is tolerated by music listeners. Therefore I have calculated this error and presented it in table 1 below.

Table 1: Equal-temperament error for common intervals

interval	just ratio	semitones	error(cents)
unison	1	0	0.000000
semitone	16/15	1	11.731285
whole tone	9/8	2	3.910002
minor 3rd	6/5	3	15.641287
major 3rd	5/4	4	–13.686286
4th	4/3	5	–1.955001
5th	3/2	7	1.955001
6th	5/3	9	–15.641287
7th	15/8	11	–11.731285
octave	2	12	0.000000

Here octaves are perfect. The smallest error represented by the intervals of a fourth and a fifth (1.955001 cents) might be a comparison standard.

Custom and average nut intonation

All normal nut setups are both straight and not slanted. Therefore the average nut intonation is just that.

(1)

Δ_nut-average =

Δ_{nut-string(1)} + Δ_{nut-string(2)} + Δ_{nut-string(3)} + Δ_{nut-string(4)} + Δ_{nut-string(5)} + Δ_{nut-string(6)}

In these spreadsheet calculations, the G string appears to be the primary violator (as everyone who plays already knows) for the nut. Yet it is still less than the reference error.

String Name	String Number	Δ_nut-optimal (mm)	Δ_nut-average (mm)	ε_nut (mm)	ε_nut (cents)
E	1	0.3	0.583333	0.283333	0.754476
B	2	0.7	0.583333	–0.116667	–0.310762
G	3	1	0.583333	–0.416667	–1.110121
D	4	0.5	0.583333	0.083333	0.221939
A	5	0.5	0.583333	0.083333	0.221939
E	6	0.5	0.583333	0.083333	0.221939

Figure 1: Fully compensated nut

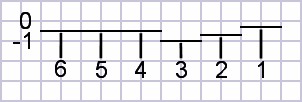Figure 2: Average compensated nut

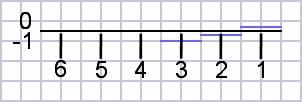Custom and average saddle intonation

Since most straight saddles are slanted to pass through the closest intonation of each string, I decided to calculate a slanted average line through the ideal values. This is done by a calculation called a linear regression, available on some scientific calculators and some internet calculators as well. My first calculation produced equation 2 below. In the table that follows the G string exceeds and the A and D strings approach the reference error.

(2)

compensation_saddle = 0.148571 × num_string + 1.58

String Name	String Number	Δ_{saddle-optimal} (mm)	Δ_{saddle-average} (mm)	ε_saddle (mm)	ε_saddle (cents)_s
E	1	1.3	1.728571	0.428571	1.141096
B	2	2.1	1.877142	–0.222858	–0.593670
G	3	3.1	2.025713	–1.074287	–2.863663
D	4	1.5	2.174284	0.674284	1.794982
A	5	1.7	2.322855	0.622855	1.658141
E	6	2.9	2.471426	–0.428574	–1.141856

Figure 3: Linear regression plots average saddle line through ideal points.

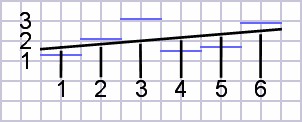Comparison with special G compensation

With the realization that the G string is a difficulty, many saddles are straight except for a customized G intonation. A calculation without G produces equation 3 below which is more ideal for the other strings. G is now presumed exactly correct. Now all intonation error is less than that of a fifth interval.

(3)

compensation_saddle = 0.186047 × num_string + 1.23023

String Name	String Number	Δ_{saddle-optimal} (mm)	Δ_{saddle-average} (mm)	ε_saddle (mm)	ε_saddle (cents)
E	1	1.3	1.416277	0.116277	0.309669
B	2	2.1	1.602324	–0.497676	–1.326036
G	3	3.1	3.100000	0	0
D	4	1.5	1.974418	0.474418	1.263122
A	5	1.7	2.160465	0.460465	1.225985
E	6	2.9	2.346512	–0.553488	–1.474808

Figure 4: Linear regression plots average saddle line through all points except G.

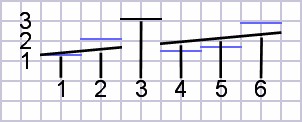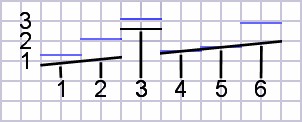
Example error of a misplaced bridge

My need to re-setup my guitar's intonation likely resulted from an error in the factory placement of the saddle. Examination of my guitar's saddle shows little or no additional intonation for strings A and D. Therefore shifting the previous compensation values forward by an amount producing correct intonation for these strings (≈ –0.5mm) will allow evaluation of intonation error that I considered objectionable. The result is excessive error for the B and E(6) strings. G would have been worse if it had not had a special factory setback.

Figure 5: Custom saddle intonation shows little additional compensation for the A and D strings.

()

compensation_saddle = 0.755812 × num_string + 1.23023

String Name	String Number	Δ_{saddle-optimal} (mm)	Δ_{saddle-average} (mm)	ε_saddle (mm)	ε_saddle (cents)
E	1	1.3	0.941859	–0.358141	–0.954149
B	2	2.1	1.127906	–0.972094	–2.591049
G	3	3.1	2.625582	–0.474418	–1.264044
D	4	1.5	1.500000	0.000000	0.000000
A	5	1.7	1.686047	–0.013953	–0.037163
E	6	2.9	1.872094	–1.027906	–2.739930

Figure 6: Factory compensation in error by ≈ –0.5mm.

Final remarks

I have read that an intonation with correctly placed straight nut and saddle (except for a G setback) is musically pleasing to all but a few. Only some sensitive individuals.benefit from a custom intonation. In my case I had the misfortune of a misplaced bridge and the fortune that it was placed correctly for a custom intonation to fall in the range of a normal saddle blank.

Disclaimer: Principle is valid for all guitars, however the exact data will be different for non-classical ones.

¹See related article: Custom Intonation.

Document History
March 15, 2018 Created.