Guitar Shape

Mathematical modeling of guitar shape leads to modeling program

Introduction

Some time ago I wondered if the shape of a classical guitar was mathematical and further if a mathematically modeled shape would be better in some way. I imagined this to be a polar plot.

Manual Attempts

When I began to explore these ideas, I first tried for a peanut (or hourglass) shape with the following equation and succeeded. This resulted in upper and lower bouts of same width with the expected waist in between.

(1)	r = a₀ + a₂cos2θ

I already had in mind that if I added a₁cosθ to the equation the lower bout could be larger than the upper.

(2)	r = a₀ + a₁cosθ + a₂cos2θ

Now the width of the outline was unavoidably narrow relative to the length without some further change. The required change was to stretch the y axis of the polar plot.

(3)	x = r·cosθ
(4)	y = y_mult·r·sinθ

Now that could get the right bout widths, the outline seemed too roundish. Adding a sixth harmonic then allowed the familiar shape with considerable tinkering with the coefficients.

(5)	r = a₀ + a₁cosθ + a₂cos2θ + a₆cos6θ

Computer solution

When I came to want a program to calculate the coefficients and plot the curve, I was stuck on the idea of an empirical method of refining the coefficients but failed to imagine a final algorithm. Then I thought of the min/max algorithm used to calculate digital filters and thought it right.

Min/Max algorithm process

User specifies length, lower bout, waist, and upper bout dimensions and a₄ and a₆ coefficients
Choose reasonable θ values for minimum and maximum points
Calculate coefficients a₀, a₁, and a₂ from current min/max θ values by solving simultaneous linear equations.
Find actual min/max points for next calculation.
Repeat 3 and 4 until convergence.

Equations on which simultaneous linear equations are based

r = a₀ + a₁cosθ + a₂cos2θ + a₃cos3θ + a₄cos4θ + a₅cos5θ + a₆cos6θ
x = r·cosθ
y = r·sinθ/a_y
r = a_y·y/sinθ
a₀ + a₁cosθ + a₂cos2θ + a₃cos3θ + a₄cos4θ + a₅cos5θ + a₆cos6θ - a_y·y/sinθ = 0
Length = 2(a₀ + a₂ + a₄ + a₆)

Matrix input to Gaussian elimination

a₀	a₁	a₂	a_y

2	0	2	0	Length – 2(a₄ + a₆)
1	cosθ₀	cos2θ₀	–Lower/sinθ₀	–(a₃cos3θ₀+ a₄cos4θ₀ + a₅cos5θ₀ + a₆cos6θ₀)
1	cosθ₁	cos2θ₁	–Waist/sinθ₁	–(a₃cos3θ₁ + a₄cos4θ₁ + a₅cos5θ₁ + a₆cos6θ₁)
1	cosθ₂	cos2θ₂	–Upper/sinθ₂	–(a₃cos3θ₂ + a₄cos4θ₂+ a₅cos5θ₂ + a₆cos6θ₂)

Program and its operation

Program name is guio.exe

Download program version 1.4.0 (New version, adds new functionality, see document history)
Download program version 1.3.1. (Old version)
Download program version 1.3.0. (Old version)
Download program version 1.2.0. (Old version)
Download program version 1.1.0. (Old version)
Download program version 1.0.0. (Old version)

EULA (End user license agreement found in about box of program).

I retain copyright. You may freely use this program for personal, non-commercial, use (that is you cannot offer it for sale). You may share it with others as long as it is provided to them complete and unmodified as you got it from my website.

Because this program is free, although it works, I do not guarantee its operation or application.

Run program and a default program shape appears.

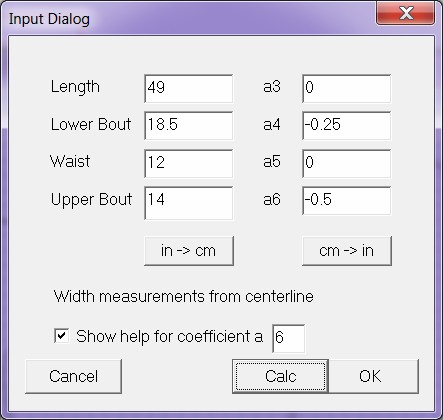
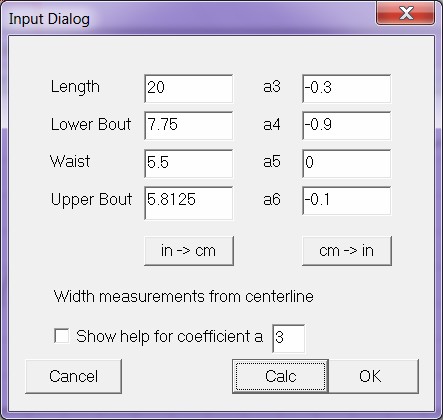
Menu->Edit->Input Shape brings up dialog to define your own shape loaded with default parameters.

Figure 1: Input Shape dialog.

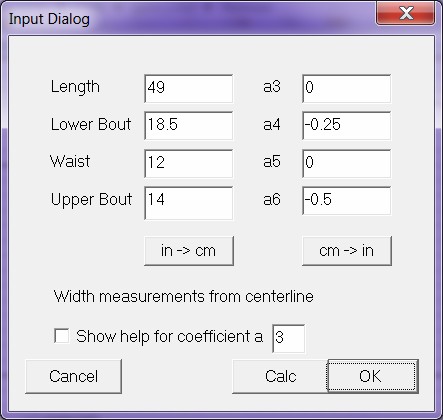Enter all required values experimenting with small values of a₄ and a₆.
in->cm and cm->in buttons convert units.
Press Calc to calculate and draw shape.
Press OK to do the same and exit dialog.

Figure 2: Guitar outline in horizontal orientation

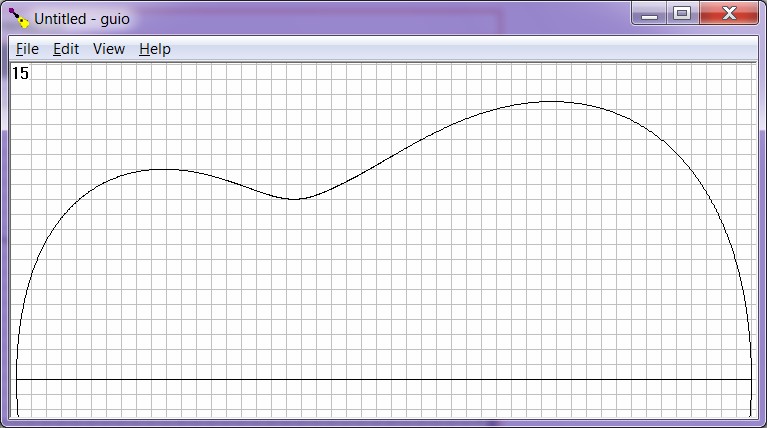Menu->View->Vertical toggles between vertical and horizontal modes with vertical mode indicated by check mark.

Figure 3: Guitar outline in vertical orientation

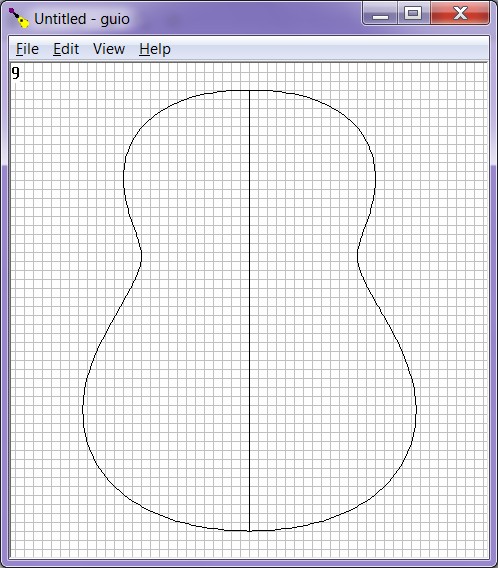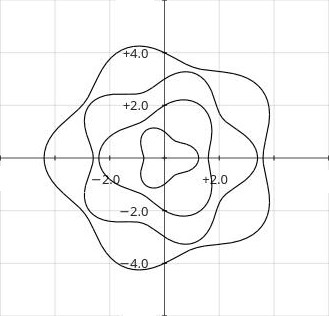
Help in adjusting coefficients a₃ through a₆

Note: These plots relate to horizontal guitar shape drawing. Use with vertical drawings would rotate the help plots 90° clockwise.

A₃ through a₆ should only have small experimental values. Figure 4 below shows positive and negative values of a₄ and a₆ added to circles to help you to understand their effects. Starting from the inside working out they are:

+ a₄.
– a₄.
+ a₆.
– a₆.

Figure 4: Graph of the effects of coefficients a₄ and a₆.

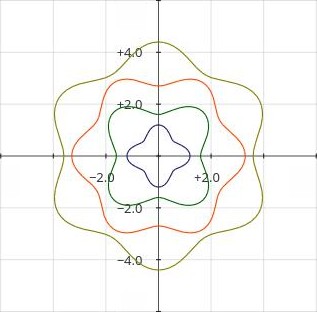Figure 5 below shows positive and negative values of a₃ and a₅ added to circles to help you to understand their effects. Starting from the inside working out they are:

+ a₃.
– a₃.
+ a₅.
– a₅.

Figure 5: Graph of the effects of coefficients a₃ and a₅.

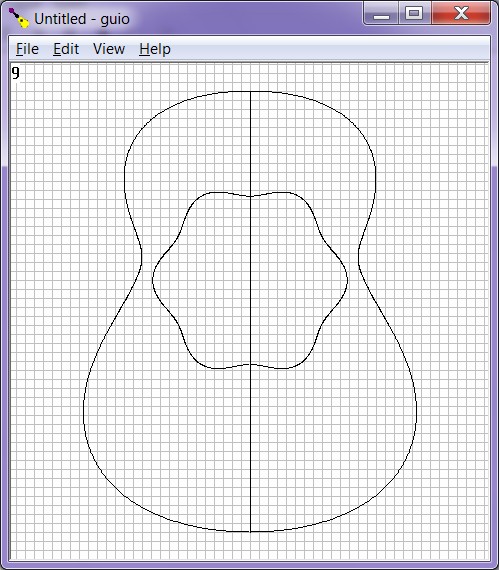
Beginning in program version 1.4.0 these help plots can be displayed inside the guitar shape.

Enter the Input shape dialog ( Menu->Edit->Input Shape ).
Click check box Show help for coefficients a_.
Enter the coefficient number for which help sought in the edit box at the end of the same sentence.
Click Calc to update the shape and show help figure.

The help plot displayed is centered with the guitar shape to have direct relevance. The plot is inverted if the current coefficient is negative from its positive form just as represented above. Any visible soundhole or fingerboard plot will be suppressed while help is on.

To turn help off:

Uncheck the previously activated check for the coefficient help from the Input shape dialog,
or turn off from menu ( Uncheck Menu->Help->Coefficient help ).

Figures 6-8: Input shape dialog with help activated for coefficient 6, and horizontal and vertical plots with help figure shown.

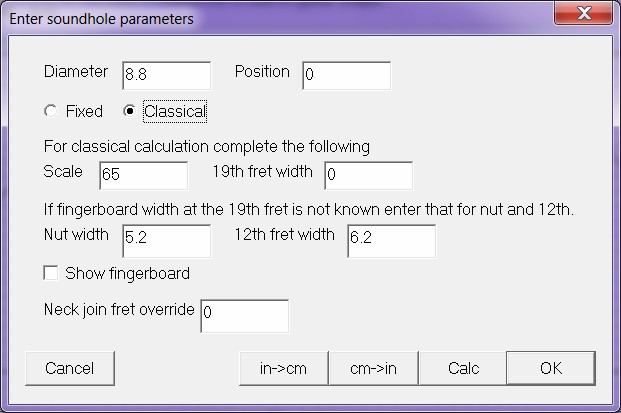
To add a soundhole to drawing

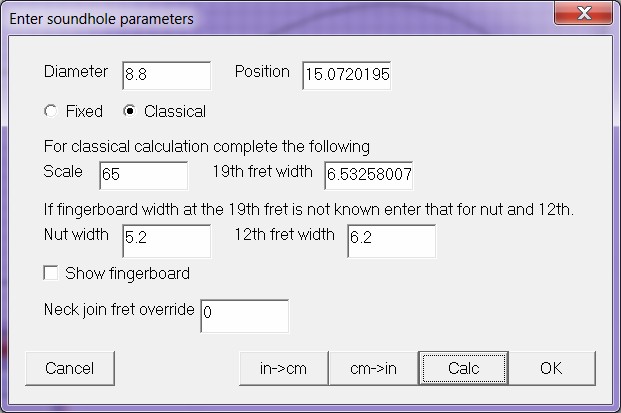
Menu->Edit->Input Soundhole brings up dialog to define or calculate a soundhole to add to guitar shape..

Fixed calculation: Enter Diameter and Position for a fixed calculation (Position is measured from neck end of body).
Classical calculation: Enter Diameter, Scale, and Fretboard/Fret width at the 19th fret (Position is calculated from these) or
Classical calculation: Enter Diameter, Scale, and Fretboard/Fret width at the nut and 12th fret (19th fret value are calculated from these.).

The classical hole position is calculated so that the hole intersects the 19th fret so as to put the middle third of that fret inside the hole. Please double-check the position of the hole by your normal methods if the drawing finds actual use.

Figures 9 and 10: Soundhole dialog before and after classical calculation.

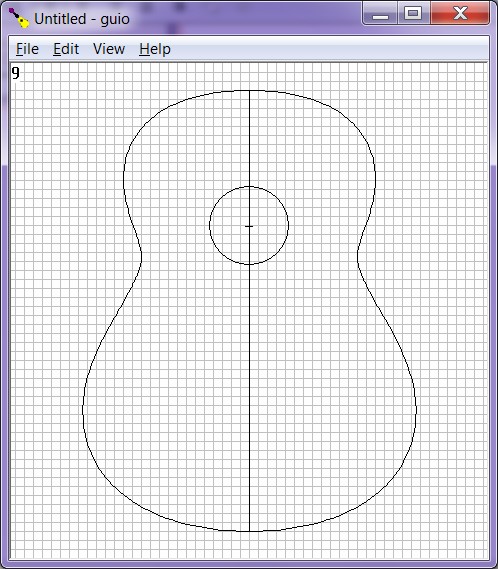
Figure 11: Guitar shape with soundhole added.

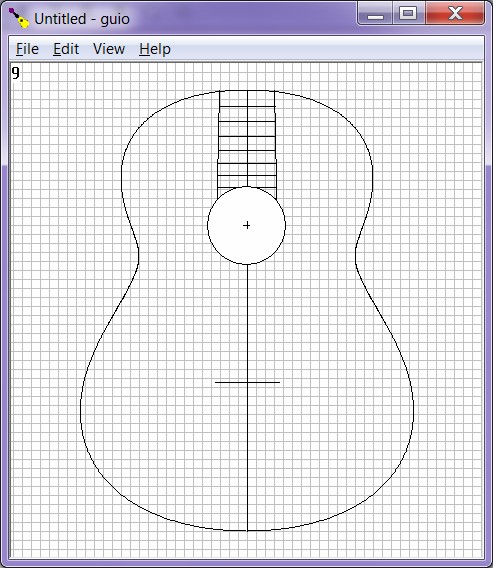
Fingerboard display

Menu->View->Fingerboard will display fingerboard (and uncompensated saddle position) if scale and fingerboard width at nut and 12th fret were entered correctly in Soundhole dialog. The fret at the jeck join is not plotted to prevent interference with display of shape. The program presumes neck join at 12th fret for a classical soundhole calculation and 14th fret for otherwise. A fingerboard can only be shown if a soundhole is already displayed. This function is to help position a steel-string soundhole relative to the highest fret or to visually verify the correct placement of the classical soundhole relative to the 19th fret.

Soundhole dialog functions for fingerboard

Fingerboard can now be activated from the Soundhole dialog when the soundhole and fingerboard are calculated.
Neck join fret override edit control can now override the default 14th fret join to the body for the fixed calculation (Left blank is as if 14 entered).

Caution: Fingerboard display may not have enough resolution to place frets accurately and is only for use in overall design. I think 100 dots/cm (254 dots/in) or more – as indicated in upper left corner – would be required for accurate fret placement.

Figure 12: Vertical guitar shape with soundhole and fingerboard added.

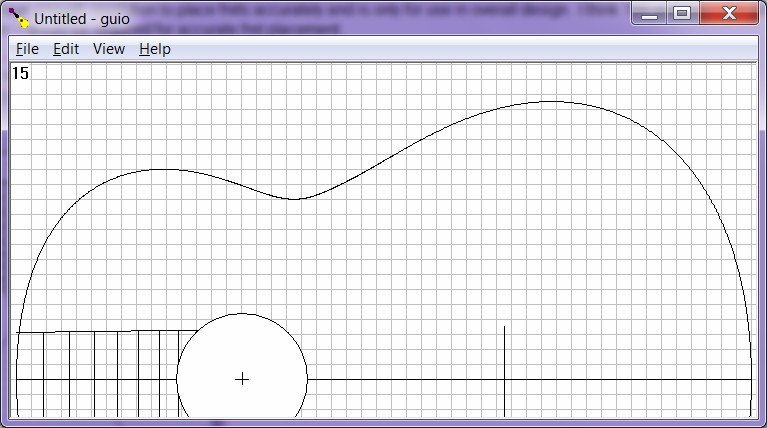
Figure 10: Horizontal guitar shape with soundhole and fingerboard added.

Miscellaneous functions

Menu->View->Side Length will display a popup dialog showing length of one side.

Figure 11: Program with Side Length dialog popped up.

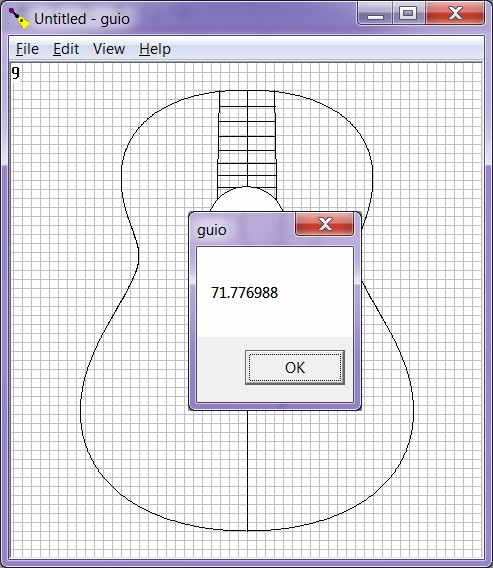Menu->View->Show Data will print primary parameters on upper left of plot. In smaller window sizes will overlap drawing.

Figure 12: Guitar shape data displayed.

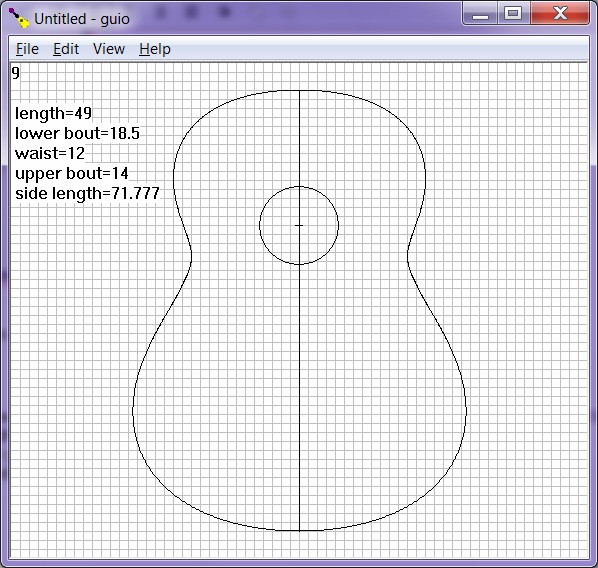Additional program notes

Units for soundhole and guitar shape must be the same. If using different units a conversion must be made at some point. This seems most likely to arise from body dimensions in inches but a scale length in centimeters.
Use centimeters and not millimeters for metric units or grid would be too tight and the resulting dots per millimeter too small to be useful.
Conversions provided in input dialogs only affect soundhole or shape variables.

To convert the entire drawing do so from the edit menu.

Menu -> Edit -> in->cm
Menu -> Edit -> cm->in

Lutherie use

For those who want life sized drawings of guitar shapes the number displayed in the upper left hand corner of the plots indicates the number of pixels per unit measure. Then follow this procedure.

Maximize program to get greatest plot resolution.
Alt-PrtSc with program selected to get its image.
Paste into a graphics program.
Scale the image to the indicated dots per unit.

In GIMP this is done as follows:
Menu->Image->Scale Image
Change X resolution and Y resolution to <your value> pixels/in (or pixels/cm)

Use graphics program to create sub-images that when printed can be taped or glued together to create a complete blueprint. (guitar bodies are larger than standard letter paper.)

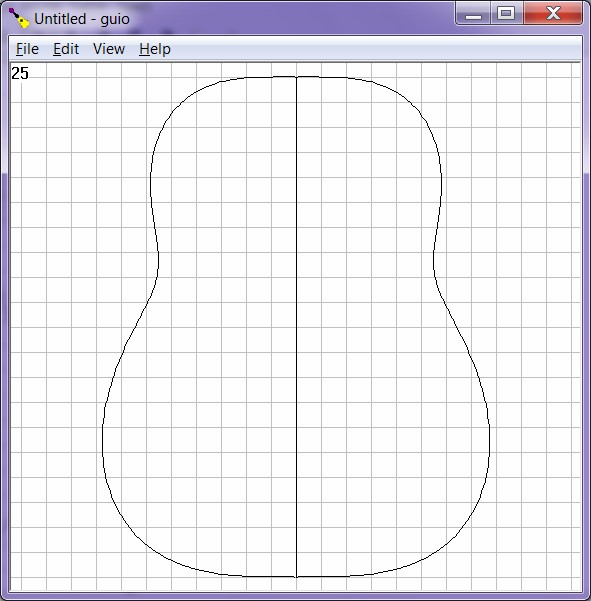
Dreadnoughts too

Although I originally sought to model the Spanish guitar the following shows an attempt at a dreadnought. The addition of coefficients a₃ and a₅ to the new program (version 1.1.0) enable a shape flat at neck and tail as shown below.

Figures 13 and 14: Input and results of attempt to model a dreadnought.

Document History
July 24, 2018 Created.
August 21, 2018 Added additional coefficients a₃ and a₅ to program to add more versatility (i.e. to emulate more possible steel-string shapes). Added a soundhole plot.
August 21, 2018 Added comment clarifying orientation of a₃ - a₆ help plots.
November 28, 2018 Program version 1.2.0. Added fingerboard, data, and side length displays. Internal changes increase resolution of shape plot and reliability of program.
December 5, 2018 .Program version 1.3.0. Extended horizontal guitar outline for improved appearance. Added neck joiin fret override for fixed calculation. Now can activate fingerboard from Soundhole dialog. Made corrections to figure titles.
December 5, 2018 Program version 1.3.1. Added more input validation and error checking to Soundhole dialog.
January 10, 2019 Program version 1.4.0 Added graphic help for coefficients..