One-Bend Amplifier

Part 5: Set bias for class B/AB and evaluate results

Introduction

Because class-a amplifiers are so inefficient and often low-powered, I thought it would be interesting if the one-bend amplifier would produce similar results in an efficient class b. Now in class-b more power is possible so I sought to raise the power supply voltage to the output stage to 60V and the driver stages to 75V to support 250W into 4Ω with 50% headroom. Note that this is an evaluation not a redesign, if the results are acceptable the input and driver stages would possibly be adjusted to ensure that no components are out of their safe ranges in a later exercise.

Circuits

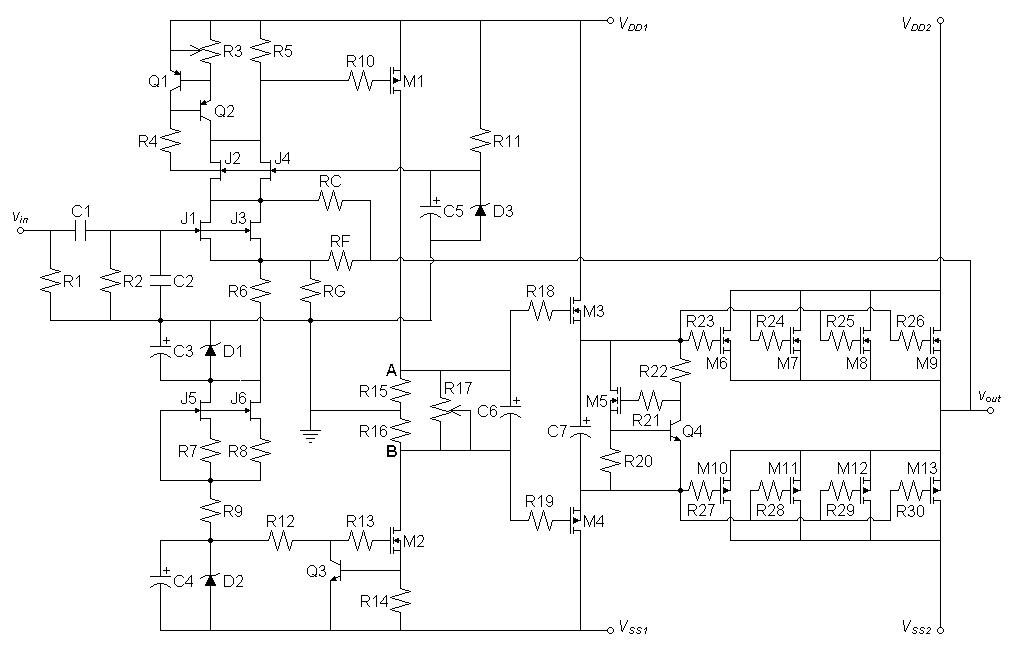
Note: Component values can be obtained from the SPICE models for now.

Figure 1: Amplifier Schematic

SPICE model

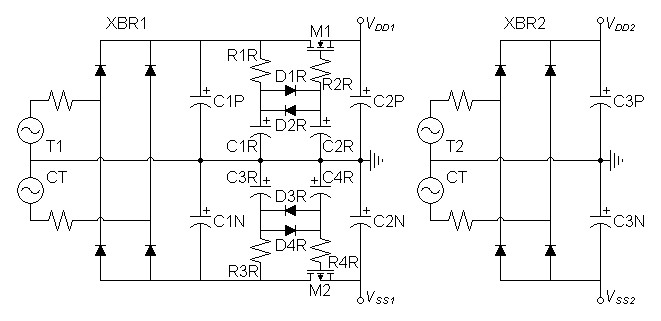
Figure 2: Regulated power supply

SPICE model

Spice Results

Forgo hum analysis for now. Instead begin with error transfer curves.

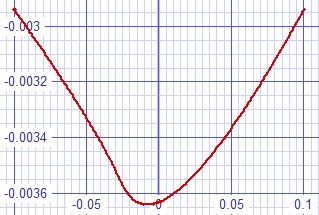
Figure 3: Small signal error curve. Shows dominance of second harmonic and some third.		Figure 4: Large signal error curve. Shows dominance of second harmonic then third.

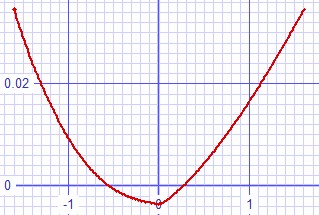These error curves plotted with convergence difficulties. I think the following distortion analysis would suggest that they are smoother than they appear.
Continue with full-power distortion analysis at 1kHz.

Fourier analysis for vout:
No. Harmonics: 16, THD: 0.0408884 %, Gridsize: 200, Interpolation Degree: 3

Harmonic	Frequency	Magnitude	Norm. Mag	Percent	Decibels

1	1000	44.7200000	1.0000000	100.0000000	0.00
2	2000	0.0181631	0.0004062	0.0406151	-67.83
3	3000	0.0019576	0.0000438	0.0043776	-87.18
4	4000	0.0003447	0.0000077	0.0007708	-102.26
5	5000	0.0004991	0.0000112	0.0011161	-99.05
6	6000	0.0000647	0.0000014	0.0001448	-116.79
7	7000	0.0003209	0.0000072	0.0007176	-102.88
8	8000	0.0000362	0.0000008	0.0000808	-121.85
9	9000	0.0002477	0.0000055	0.0005538	-105.13
10	10000	0.0000288	0.0000006	0.0000644	-123.83
11	11000	0.0001972	0.0000044	0.0004410	-107.11
12	12000	0.0000240	0.0000005	0.0000537	-125.40
13	13000	0.0001604	0.0000036	0.0003588	-108.90
14	14000	0.0000208	0.0000005	0.0000465	-126.64
15	15000	0.0001320	0.0000030	0.0002952	-110.60

Certainly we are interested in frequency response

Figure 5: Bode shows frequency response down 3dB at 524kHz

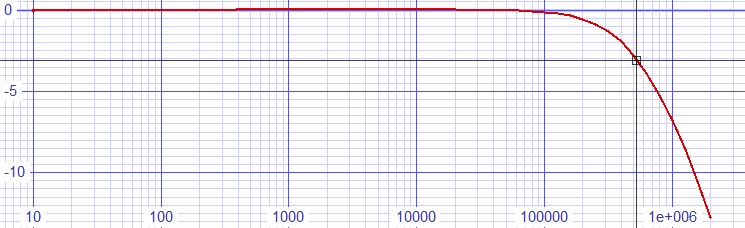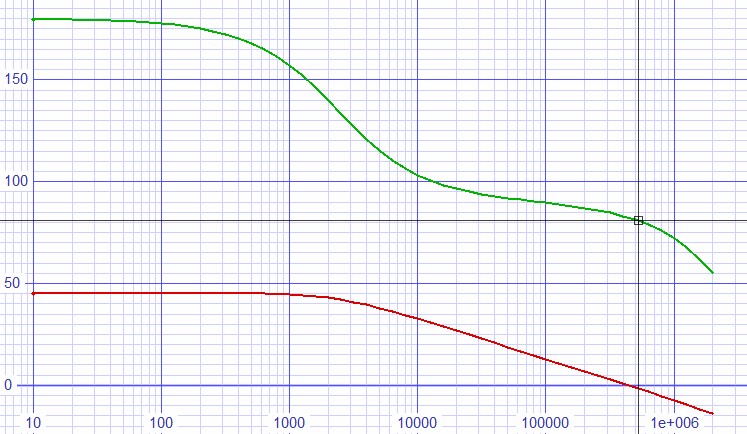
For stability the open loop phase margin at the closed-loop -3dB frequency should be more than 45º.

Figure 6: Stability analysis showing 80.9º of phase margin.

Conclusions

The desired predominance of second harmonic expected as a result of the inner feedback loop is the same as the previous class--a result. After that the harmonic profile does not taper off like class-a but rather odd-harmonics are preferred perhaps an expected result. Perhaps a less pure class-a sound would result than previously. I think the class-b version is worth further investigation.

¹Note: Raw Fourier analysis data has been processed in spreadsheet to calculate related results and reformatted.
³See related article: Floating Source-follower Regulator.

Document History
May 15, 2018 Created.