Home  │ Audio Home Page

Copyright © 2011 by Wayne Stegall
Created January 26, 2011.  See Document History at end for details.

Flicker Noise Calculations

Introduction

As a result of expanding the functionality of the Op Amp Noise Calculator, I thought it useful to do another article on noise.

For most noise calculations pertaining to electronics, it suffices to consider white noise only.  However account  of another type of noise does sometimes merit concern.  That is flicker or 1/f noise.  The power of this noise of unknown origin is inversely proportional to the frequencies of interest, distributing equal power to every octave.  This pink noise profile declines 10dB/decade or 3dB/per octave, a rate half that of the stopband rolloff of a first-order RC network.  Added root-sum-square to the white noise level also present creates a noise response break frequency below which the flicker noise rises at its characteristic rate.  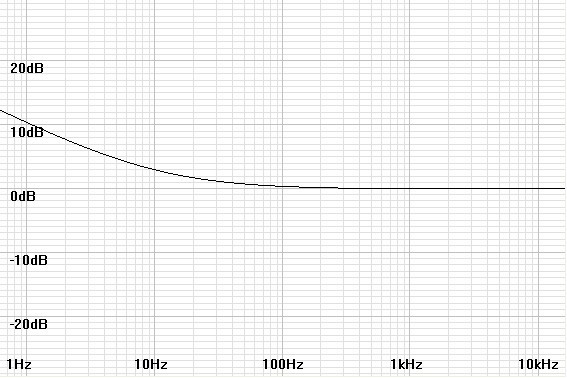This noise corner frequency is the frequency where the flicker noise is equal to the white noise specification in V/√Hz (see figure 1 below).

If you are new to noise calculations you may want to examine Simple Noise Calculations before proceeding.

Figure 1:  Noise plot shows 1/f noise rise below 10Hz noise corner from normalized white noise level

Mathematical Analysis

The specification of (f) or (f₁,f₂) next to power or voltage in these analyses indicate that these variables are functions of frequency or a range of frequencies and does not indicate a multiplication.  Multiplication will be indicated by another level of parentheses or an ×.

Because noise is always specified relative to frequency in Hz rather than radian frequency, it is well to derive the math based on f rather than ω.

The flicker power function (in W/Hz) is inversely proportional to the frequency.

(1)

pfn(f) =

k f

 The constant k is arbitrary at this point. 

Because the mean square voltage¹ and current are proportional to their corresponding power, that is v_n(f)² = p_n(f)R, then

(2)

vfn2(f) =

kR f

Because it is common to relate flicker noise to the characteristic white noise at a frequency where both are equal called the noise corner frequency (f_nc),
if we set

(3)

k =

vwn2(f) × fnc R

the equation (2) becomes:

(4)

vfn2(f) = vwn2(f)

fnc f

v_wn(f) here represents the semiconductor white noise specified V/√Hz in datasheets; v_fn(f) is specified in units of V/√Hz as well.

Integrating the 1/f function through the range of frequencies representing bandwidth gives the corresponding total mean square flicker noise

(5)

vfn-total2(f1,f2) =

∫

f2 f1

vwn2(f)

fnc  f

df

Knowing that ∫1/f df = log_e(f) = ln(f) the integral becomes

(6)	vfn-total2(f1,f2) = vwn2(f) × fnc × (ln(f2)-ln(f1))

That subtraction of logarithms is equivalent to division allows a more convenient representation.

(7)	vfn-total2(f1,f2) = vwn2(f) × fnc × ln(f2/f1)

Take the square root of total mean squared voltage noise to get total flicker noise:

(8)

vfn-total(f1,f2) = vwn(f)

fnc × ln(f2/f1)

Adding It Up

After calculating flicker noise it is well to add up all noise sources.  Flicker noise adds root-sum-square as does white noise.
Total white noise specified as a function of voltage noise per √Hz and bandwidth is:

(9)

vwn-total(f1,f2) = vwn(f)√B = vwn(f)

f2 - f1

Square total white noise and flicker noise and add them to get total mean square noise:

(10)	vn-total2(f1,f2) = (vwn2(f) × (f2 - f1)) + (vwn2(f) × fnc × ln(f2/f1))

Take square root of total mean squared voltage noise to get total noise:

(11)

vn-total(f1,f2) = vwn(f)

(f2 - f1) + fnc·ln(f2/f1)

A Statistical Diversion

The statistical chance that noise voltage level will take a certain instantaneous level follows the pattern of a Gaussian distribution.  This is the familiar bell curve.  The RMS noise value corresponds to one standard deviation (written 1σ).  This is because the standard deviation calculation is itself an RMS calculation of the variance of the changing variable relative to the mean (0V or 0A in the case of noise).   A peak to peak ±1σ contains 68.3% of statistically possible values, a value that differs from the 70.7% value we expect from a RMS calculation of a sine wave.  This is because the sine wave, not being random, does not have a Gaussian distribution.  That ±3σ contains 99.9% of all possible levels represents a peak-to-peak signal excursion of 6σ, leaves the peak value to deviate only 3σ.  These standard deviation factors become conversion factors to convert between RMS, peak, and peak-to-peak noise specifications: vn(rms) = vn(peak) ÷3 = vn(p-p) ÷6 vn(peak) = vn(rms) ×3 = vn(p-p) ÷2 vn(p-p) = vn(rms) ×6 = vn(peak) ×2

Figure 2:  Plot of noise Gaussian showing relationship to different signal designations.

Reading Datasheets

Datasheets often give flicker data in a form other than the most useful noise corner frequency (f_nc).  A midband noise specification will be given for the white noise.  A single specification at a lower frequency will contain flicker and white noise from which f_nc can be calculated.  Alternatively, a noise total for a range of frequencies below the white noise specification will be given.

First, if necessary convert any peak-to-peak specifications to RMS by dividing by 6 (refer to note on conversions above), then calculate the noise corner frequency from equations (13) or (14) below.

Derive the formula for f_nc based on a single low  frequency specification.
First, solve the 1/f formula of equation (4) for f_nc.

(12)

fnc =

vfn2(f) × f vwn2(f)

Substitute the subtraction of the square of the white noise specification from the total noise specification for the square of the flicker noise specification (all in V/√Hz) to yield the final formula.

(13)

fnc =

(vn-total2(f) - vwn2(f)) × f vwn2(f)

Derive the formula for f_nc based on a noise total for a range of frequencies.
Solve equation (11) for f_nc to get formula deriving f_nc from a noise specification through a range of frequencies.

(14)

fnc =

(vn-total(f1,f2)/vwn(f))2 + f1 - f2 ln(f2/f1)

Example

Take the following specifications from the LSK170 datasheet:

• Midband white noise specification, v_wn(f) = 0.9nV/√Hz at 1kHz
• Low-frequency noise specification, v_n-total(f) = 2.5nV/√Hz at 10Hz  (both are labeled e_n²)

For this JFET, calculate the total white noise from 20Hz to 20kHz, the noise corner frequency, the total flicker noise from 20Hz to 20kHz, then the total noise from 20Hz to 20kHz.

From equation (9) calculate total white noise:

vwn-total(f1,f2) = 0.9nV/√Hz

20kHz - 20Hz

= 0.9nV/√Hz

19980Hz

v_wn-total(f₁,f₂) = 0.9nV/√Hz × 141.351√Hz = 127.216nV

From equation (13) calculate noise corner frequency.

fnc =

((2.5nV/√Hz)2- (0.9nV/√Hz)2) × 10Hz (0.9nV/√Hz)2

=

(6.25a(V2)/Hz - 0.81a(V2)/Hz) × 10Hz 0.81a(V2)/Hz

fnc =

(5.44a(V)2/Hz) × 10Hz 0.81a(V)2/Hz

= 6.71605  10Hz = 67.1605Hz

From equation (8) calculate total flicker noise.

vfn-total(f1,f2) = 0.9nV/√Hz

67.1605Hz × ln(20kHz/20Hz)

= 0.9nV/√Hz

67.1605Hz × ln(1000)

vfn-total(f1,f2) = 0.9nV/√Hz

67.1605Hz × 6.90776

= 0.9nV/√Hz

463.928Hz

v_fn-total(f₁,f₂) = 0.9nV/√Hz × 21.539√Hz = 19.3851nV

Calculate total noise from total white noise and total flicker noise by root-sum-square:
v_n-total²(f₁,f₂) = (127.216nV)² + (19.3851nV)² = 16.1839f(V²) + 375.782a(V²) = 16.5597f(V²)
v_n-total(f₁,f₂) = 128.684nV

Final Thoughts

The example above illustrates an important point.  The 128.684nV total after adding flicker noise to the white noise total of 127.216nV is only an increase of 0.1dB.  It is often safe to ignore flicker noise and calculate white noise only if the noise corner frequency is near the lower end of the band calculated.

You can tinker with flicker noise calculations with the Op Amp Noise Calculator.

¹Mean square values are squared rms values.
²E is sometimes used to represent the voltage variable rather than v, derived from voltage's original name, electromotive force or emf.  The reason may lie with combination electro-mechanical systems, where v is in conflict for use as voltage and velocity, one of which has to be changed.  E is not used in place of Volt as a unit however.  V is the preferred variable for electronics-only applications because e is also the base of the natural exponential, a common function in electronics mathematics.  The similar appearance of eⁿ and e_n, at least in quick reading, could create problems that that use of v for emf would alleviate.

Document History
January 26, 2011  Created.
January 26, 2011  Changed (f1-f2) to (f1,f2) to better represent dual function arguments and added an additional comment at the end.
January 26, 2011  Corrected a name discrepancy that made equations (11) and (14) seem inconsistent.
January 27, 2011  Made minor improvements for clarity and grammar.