Home  │ Audio Home Page

Copyright © 2011, Free use of program governed by statement in About dialog which is repeated below.
Updated June 2, 2012.  See Document History at end for details.
SPICE verified.

FETCurve

 

Introduction

In the context of desiring to match or scale FET parameters for the purpose of distortion cancelation, it becomes desirable to calculate these parameters.  Few would have access to transistor testers for their high cost.  Here I show how these parameters can be calculated from measurements made with just a power supply and a multimeter and provide a dedicated calculator to make them.
 

Calculations

These calculations are exact for enhancement MOSFETs.  The program makes minor adjustments for JFET's depletion mode bias range.

Simple Calculations are based on the idea that the V_GS measured with the highest bias resistor is approximately V_T.  R_BIAS determining V_T would have to be very high compared to any anticipated circuit bias like 1MΩ.  The other measurement would then determine k_n (or KP in SPICE terms).

If V_GS1 ≈ V_T then

(1)	ID2 =	VBIAS - VGS2 RBIAS2
(2)	kn =	ID2 (VGS2 - VT)2

Two-Point Calculations mathematically fit a curve to the data instead.  Three data points are usually required to define a second order polynomial.  Two data points suffice because a constant preexisting boundary condition satisfies the function of the third data point.  That di/dv = 0 when i = 0 at V_T defines this boundary condition.

If the MOSFET equation

(3)	ID = kn(VGS - VT)2

is rearranged in the form

(4)

ID kn

+ VT = VGS

A pair of simultaneous non-linear equations suitable for solving for k_n and V_T can be written:

(5)	ID1 kn	+ VT = VGS1
(6)	ID2 kn	+ VT = VGS2

The following substitutions in the rearranged MOSFET equation

(7)	x0 =	1 kn
(8)	x1 =	VT
(9)	aX0 =	IDX
(10)	aX1 =	1
(11)	aX2 =	VGSX

where X is the data point and equation number, yields solvable simultaneous linear equations in the form of:

(12)	a10x0 + a11x1 = a12
(13)	a20x0 + a21x1 = a22

or in standard matrix form:

(14)

a10 a11 a12 a20 a21 a22

Continuing with the substitutions in the matrix:

(15)

ID1 1 VGS1       ID2 1 VGS2

By matrix reduction, the matrix is transformed to diagonal format with the last column containing the results:

(16)

1 0       1 kn 0 1 VT

Because the reduced a₂₂ term returns V_T in its final form, it remains only to solve for k_n from the reduced a₁₂ term.

(17)

kn =

1 a122

Calculator

Based on above calculations, I am offering a simple calculator for download.  It is tested in Windows XP, Windows 98, and under Linux using Wine (Windows Emulator)¹ as well.

EULA

I retain copyright.  You may freely use this software for personal, non-commercial, use (that is you cannot offer it for sale).  You may share it with others as long as it is provided to them complete and unmodified as you get it from this website.  Because this program is free, although it works, I do not guarantee its operation or application

Download

	Download FETCurve 1.2.1.zip (13KB)
	Download FETCurve 1.1.0.zip (12KB)
	Download FETCurve 1.0.0.zip (12KB)

After download, copy the executable into the desired directory.  You will have to manually create links on the desktop or the start menu, as you desire.

Instructions

(These are to serve in place of a program help file)

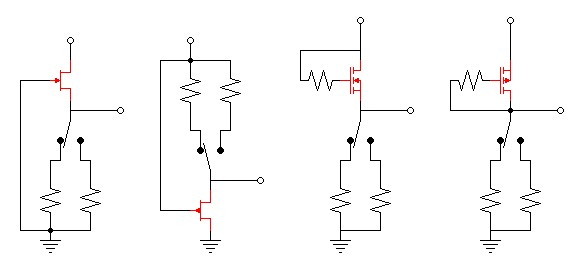
1.  Test Circuit Setup

Enhancement MOSFETs tested must be connected so that V_BIAS drops across the selected bias resistor and V_GS in series.  JFETs tested must be connected with selected bias resistor placed between gate and source and sufficient voltage applied to the drain to ensure device is biased out of its linear range into saturation.  Depletion MOSFETs can be tested the same as JFETs.  If depletion MOSFETs are tested with enhancement bias, drain voltage cannot be connected with gate voltage as the enhancement circuit, but sufficient voltage above gate voltage must be applied to the drain to ensure device is biased out of its linear range into saturation.  Experimentation may be required to determine the best R_BIAS values.  At least use values one above and one below the operating point of your expected circuit.

Figure x:  Example Test Circuits.                   Depletion Mode                                          Enhancement Mode         NJFET                      PJFET                        NMOSFET                PMOSFET

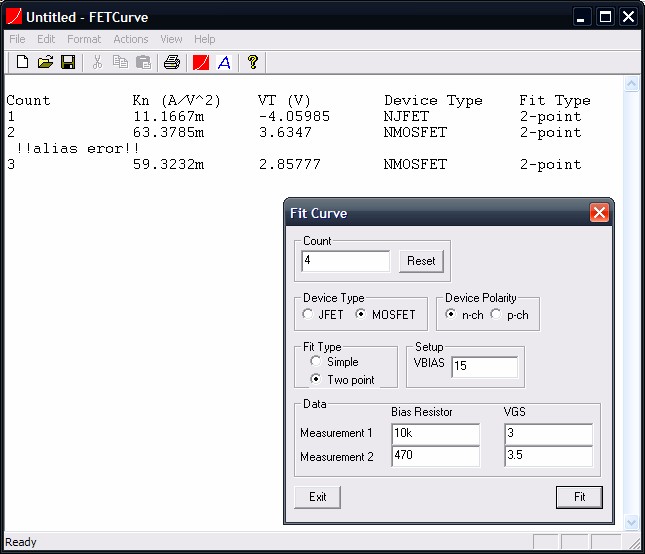
2.  Soft ware Operation

• Program centers around text editor which recieves the measurement logs.

• Execute Fit Curve dialog by selecting Actions/Fit Data from menu or clicking related toolbar function ().

• Count will increment by one for each curve fit.  Count can be preset by entering a value into its edit control or reset to one by pressing Reset.

• Select Device Type, Device Polarity, and Fit type.

• Enter V_BIAS used.  This entry will not affect JFET calculations.

• Enter R_BIAS and V_GS for each measurement.  Values may be entered with the SI prefixes in the following chart.  Program only uses the absolute values of the entered V_GS, polarities are determined instead by the device type and polarity.  For this reason, depletion mode MOSFETs must not be tested with bias points that would give both positive and negative values for V_GS.
  

• When data is entered press Fit button and calculations will appear in the text editor under the Fit Curve dialog each appended as a separate line.  Numeric entry boxes detect common typing errors and tag them with ? after the error dialog is dismissed.  Improperly formed data can produce an error result, in which case you should examine the consistency of your test circuit and measurements.
  

• After measurements are complete press Exit to leave dialog.  The data then may be commented as you desire before saving to a file.

SI prefixes
Factor Name Symbol 1024 yotta Y 1021 zetta Z 1018 exa E 1015 peta P 1012 tera T 109 giga G 106 mega M 103 kilo k		Factor Name Symbol 10-3 milli m 10-6 micro µ 10-9 nano n 10-12 pico p 10-15 femto f 10-18 atto a 10-21 zepto z 10-24 yocto y

SPICE verification

Program is now SPICE verified.  SPICE verification was held up by confusion of transconductance factor k_n with SPICE tranconductance bulk factor KP.

(18)

kn =

KP 2

×

W Leff

Previously, SPICE verification did not seem necessary because of mathematical correctness to textbook MOSFET equation.

SPICE model for JFET test set.
SPICE model for enhancement MOSFET test set.

Software Input Limitations

Because I did not want to accidentally restrict the usefulness of the program, I have not placed any range limits on the inputs to the program.  At some later time I may place thoughtful and modest input limitations.  Until then, the user is responsible to input well-formed input data.  Therefore, there are a few pitfalls to beware:

• Choice of two bias resistors should be different.  If not, the resulting linear equations will be identical and therefore unsolvable.  Even, if the bias resistors are different but close, accuracy of results could suffer.
• Identical V_GS values are implausible and result in infinite k_n.
• The MOSFET equation defines a entire symmetrical parabola but only uses a half on one side of V_T.  If the data is misformed to place a solution in the undefined region of the parabola, the results will be invalid.  This would occur as a result of accidentally swapping V_GS1 and V_GS2. or calculating MOSFET data as if JFETs or the reverse.  As of version 1.1.0, the program now tags the calculated results with the error message !!alias error!! if this error is detected.
  
• Do not choose a zero bias resistor for one bias point of a JFET thinking to represent a data point at I_DSS, as a non-zero voltage across the resistor is needed for the calculations.
  

It would be well to have or gain a good understanding of FET characteristics to use and interpret the output of this program.

Can it run on Windows 95? 

Windows 95 may not have the shared Visual C++ 6.0 dlls needed to run this program.  If you have any problem that implicates a missing file, mfc42.dll or msvcrt.dll, download here, and copy into the directory with the program or into the windows system directory (c:\windows\system\  or c:\windows\system32\  whichever contains system dlls).

 

 

¹Specifically, Wine version 1.2.2 under Kubuntu 10.10 Maverick Meerkat.  You will have to copy mfc42.dll and/or mfc42u.dll to ~/.wine/drive_c/windows/system32 directory for proper operation.

Document History
June 26, 2011  Created.
June 26, 2011  Added section on software input limitations specifying some data pitfalls, made minor improvements, and clarified a wordy sentence.
May 31, 2012  Added SPICE verification.  Updated program to version 1.1.0 to flag alias error and to show k_n for transconductance factor to avoid confusion with SPICE parameter KP.
June 2, 2012  Updated program to version 1.2.0 adding input checking for numeric entries.  Immediatedly released version 1.2.1 to allow negative number entry.