Home  │ Audio Home Page

Copyright © 2014 by Wayne Stegall
Updated May 27, 2014.  See Document History at end for details.

Differential Equalization

Introduction

An equalized differential circuit is redundant: one side repeating the components found on the other.  The following transformation allows many of those components to be shared.

Concept

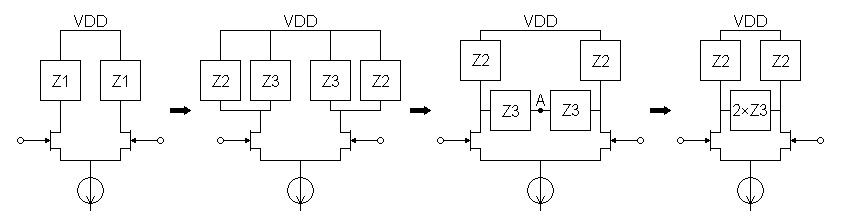
I figure 1 following, if Z₁ can be subdivided into parallel components Z₂ and Z₃, matching parallel legs of the circuit from each side can cross connect, halving the number of components for that leg.  The key to understanding the transformation is to note that node A where the two matching parallel legs connect is a virtual ac ground.  This is because the circuit is topologically symmetrical with opposite polarity signals on each side ensuring that the dc voltage component always remains zero.  Only the connection to another ac ground (V_DD in this case) can be reconnected to make a virtual ground in this way.

Figure 1:  Schematic shows step-by-step transformation of redundant differential circuit to one with less components.

Derivation

The empirical derivation of the transformation seems reasonable enough.  However there are reasons not to accept it without proof.  For one thing, it is immediately obvious that transformed circuit is not equivalent to the original for a single-ended input.  The impedance of the circuit seen by the output of one transistor depends on the opposite polarity of ac signal being driven at the output of the second transistor.  I deemed necessary to set up an equation based on the principle of superposition:  that is to add the voltage contribution to the transistor ac output voltage of each current together.  Then it remains to solve for the equivalent impedance.

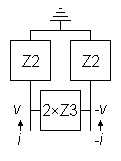
Figure 2:  AC schematic of transformed circuit

(1)

v = i(Z2 || (Z2 + 2Z3)) – i

Z2 Z2 + 2Z3

(Z2 || (Z2 + 2Z3))

(2)

Zequiv =

v i

=

1 –

Z2 Z2 + 2Z3

(Z2 || (Z2 + 2Z3))

(3)

Zequiv =

2Z3 Z2 + 2Z3

Z2(Z2 + 2Z3) Z2 + Z2 + 2Z3

(4)

Zequiv =

2Z3Z2 2Z2 + 2Z3

=

Z2Z3 Z2 + Z3

=

Z2 || Z3

Examples

In practice, this transformation works best with equalization topologies that have a parallel high level structure.  For this reason, the examples I give here meet such a requirement.  The actual calculation of component values in differential RIAA circuits should use this article in conjunction with the calculations give for single-ended circuits in the main RIAA equalization article.¹  Note also, as a practical matter, that the main dc paths to V_DD have to remain connected to V_DD and not combined into the cross element.

Transformation of parallel circuits

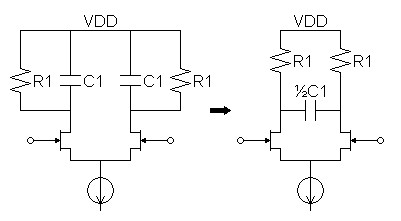
Figure 3:  Parallel lowpass filter.

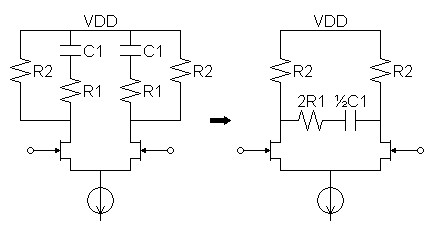
Figure 4:  Parallel-series shelf equalization circuit commonly used for first stage of two-stage RIAA equalization.

Figure 5:  Parallel-series (or passive) RIAA equalization circuit.

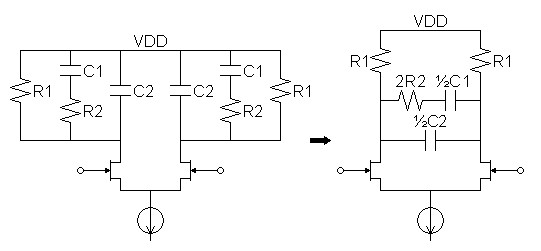
Figure 5:  Parallel-series (or passive) RIAA equalization circuit with extra 50kHz zero.

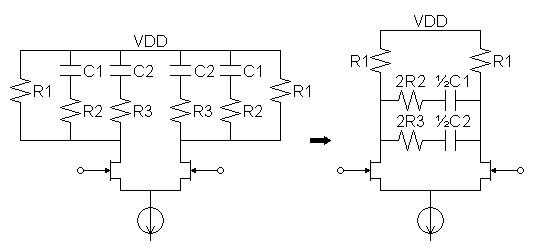
Transformation of partially parallel serial circuits

To be added later.

¹See article:  Phono Equalization Calculations.

Document History
May 27, 2014  Created.
May 27, 2014  Added a sentence and corrected some spelling.