Analog is Digital

Quantum mechanics defines quantization of analog signals comparable to that of digital audio.

Introduction

Even though analog signals are thought of as continuous, we know that some point near the atomic level that they become granular. In spite of this suspicion, we still disregard this idea because we think these affects are infinitely small. It comes as a surprise then that physics has already defined this analog granularity in specific concrete terms at least for electronic and magnetic systems. After establishing that electromagnetic radiation is emitted in discrete packets know as photons, physicists determined that all electromagnetic energy was composed of photon-sized energy quantums. Thus Plank's equation which defines the energy of an individual photon also defines discrete levels at which analog energy is quantized. This is likely related to the fact that electrons move through conductors as waves as well as particles just as photons do in transparent mediums.

Plank's Equation

(1)

E = hν

where E is a discrete packet of energy,
h is Plank's constant of 6.62606896e-34,
The Greek letter nu (ν) represents frequency in this branch of physics. (I will use the conventional f for frequency from here on.)

This equation represents a spectrum of quantization noise that rises in direct proportion to frequency. The noise corner for quantum noise is at kT/h or 6.25099THz at a temperature of ≈ 80°F. Below this frequency quantization is masked by white noise. Above this frequency white noise rolls off with an exponential lowpass function and quantum noise takes over and dominates.

The Real Resolution of Analog

The first deduction to be made is that analog resolution is not determined by the thermal noise floor as is commonly thought by those who compare it unfavorably with digital. The quantization level is well below the thermal noise floor for all frequencies relevant to audio. It might be informative to calculate white noise power and quantization noise in the audio band to see what the actual difference is. First calculate white noise.

(2)

P_whitenoise =

4kTΔf = 4 × 1.3806504e-23 × 300K × (20kHz – 20Hz) = 3.31025e-016 W

or –154.801dBW

Calculating the noise integral for white noise equated to just multiplication because its spectrum is flat. Quantization noise provides no such shortcuts. Therefore the full integral must be solved.¹

(3)

P_qn = 4

∫

20000

20

(4)

P_qn = 4

20000

20

hf²

(5)

P_qn = 2h

20000

20

f²

(6)	P_qn = 2 × 6.62606896e-34 × (20000² – 20²) = 5.30085e-025 W

or –242.757dBW

Therefore the quantization floor representing the actual resolution of an analog signal is 242.757dB – 154.801dB or 87.956dB below the white noise floor.

Comparison of Analog and Digital Processes

Next, interest seems to lead to comparing the quantization of analog signals to some appropriate modern digital reproduction chain. It will become quickly obvious why this comparison should be made to DSD.

The shape of the noise floor of both analog noise and DSD follow the same pattern: To remain flat through a region and then rise in a higher frequency region where the quantization process tends to place the noise. (See noise profiles in figures 1 and 2)
The process by which the signal moves from input to output is similar: Analog energy moves from the input to the output as discrete quantum units of energy are available to move. Similarly, input energy to a delta-sigma modulator does not move to the output until it can move in clock-duration output pulses. The net effect of both is that the energy density of the output represents the input energy and quantization is filtered out by some lowpass functionality in the receiving system.²
The claim by a physicist that the resolution of an analog system can be increased by filtering out out-of-band quantum noise leaving lower level inband quantum noise seems parallel to the idea of converting DSD to PCM by means of a digital lowpass filter.³

Figure 1: Analog noise profile in a 1kΩ resistor.

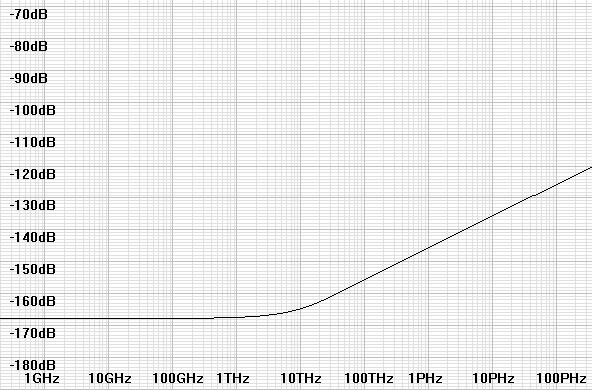Figure 2: Noise floor of a hypothetical 2nd-order analog delta-sigma modulator.

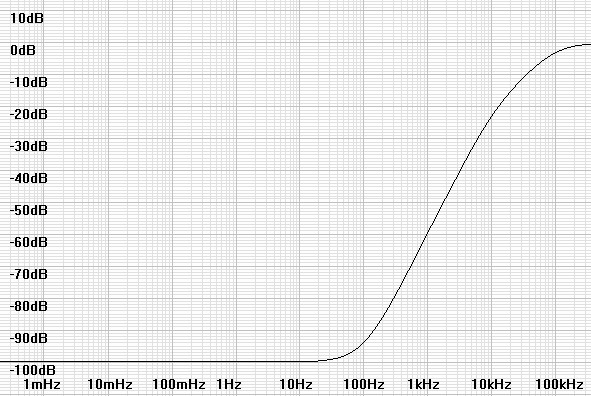Conclusion

The fact that analog is quantized at some low level boosts the idea that increasing the resolution of digital audio systems holds real hope to sound more analog.

¹Multiplication of the basic noise equations by a factor of 4 for both thermal and quantization noise seems to combine two factors of 2: one from adding negative and positive frequencies, and the other to compensate for the fact that only half of the noise power a resistor can be communicated into a matched load.
²See article Delta-Sigma Modulators.
³Jack Bybee is the physicist who makes this claim for a product that he will sell you.

Document History
May 24, 2013 Created.
May 24, 2013 Corrected format of equation 3 and renumbered equations.