Delta-Sigma Modulators

Their basic theory of operation

Introduction

It was possible that I created curiosity about delta-sigma modulators in my previous article Digital Audio Formats. To satisfy any such curiosity I describe here their method of operation. It may be useful to reread that article as a prerequisite to this one.

Digital Modulator

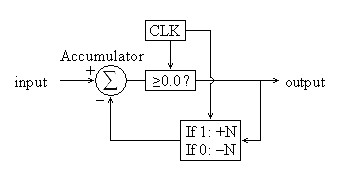
It is useful to begin by explaining a first-order digital delta-sigma modulator. To produce a bitstream with an average value proportional to an analog input (or its PCM equivalent), it is necessary to track and conserve input energy as it is output in constant pulses. In the following flowchart, the accumulator tracks this energy. Input values are added to the accumulator as they are received, the accumulator acting functionally as a digital integrator. A positive balance in the accumulator requires a positive binary output value (1) and a negative balance requires a negative binary output value (0) for proper representation. Then a constant value N is subtracted or added respectively to track the energy deployed to the output to represent the input signal. This creates a feedback loop that ensures that all of the input energy is represented at the output with some uncertainty as to which exact pulses and how many will be involved in the representation. It is assumed that the output frequency is much greater than the maximum input signal frequency so that many bits can represent each positive and negative swing. DSD and many DACs modulate the bitstream at 64x to 128x the normal 2x sampling rate specified as a minimum for PCM.

Figure 1: Flowchart of digital modulator

Figure 2: Pseudocode

main()
{

on
arrival of input sample
accumulator = accumulator + input;

on out_clock

{
if(accumulator >=0.0)
output = 1;

else
output = 0;

if(output == 1)
feedback = N;

else
feedback = -N;

accumulator = accumulator - feedback;

}

}

Noise Shaping

At first glance this algorithm seems to have a fatal flaw. 64 or 128 bits per up or down swing of a signal seems only to be able to represent the same number of discrete levels of signal. Thus 64x sequential bits would seem only to have 6 bits of equivalent PCM resolution and 128x only one bit more. However another factor is at work so that that much greater resolution is attained. There is additional room for level coding in the arrangement of any particular number of ones and zeros. This is because the actual arrangement of ones and zeros determine a short term frequency spectrum that, depending on the exact sequence can distribute the represented energy in many different ratios between the near-audible part of the spectrum and the inaudible. After lowpass filtering, which even the human ear will do, only the energy in the near-audible part of the spectrum will contribute its part to the overall level. This process falls under the topic of noise-shaping and enables a claim that a 64x bitstream can represent 20-bits of resolution at an equivalent PCM rate of 96kHz.

Analog Modulators

At this point the process of noise shaping may seem a mystery. However examination of analog delta-sigma modulators will make the nature of its operation clear. In figure 3 below, an integrator composed of the op-amp, R₁, and C₁ performs the function of the accumulator. In particular, capacitor C₁ holds and manages the input energy until it is spent at the output. The comparator then performs the decision whether the energy in C₁ should produce at any time a positive (one) or negative (zero) level on the output. The clocked D latch or flip-flop ensures that the comparator decision is held for an entire clock cycle. The feedback resistor R_F then subtracts the energy of the output pulse from the capacitor to register the current cycle's progress toward representing the input signal at the output. In contrast to the discrete tracking of energy in the digital modulator, C₁ is continuously charged by the input and output in feedback system toward the goal of always spending the energy in the capacitor toward draining it to zero volts. As with the digital modulator, this process ensures that the digital output bitstream has an average energy density that correctly represents the analog input needing only the proper analog filter to restore a scaled replica of the original input signal.

Figure 3: First-order analog modulator

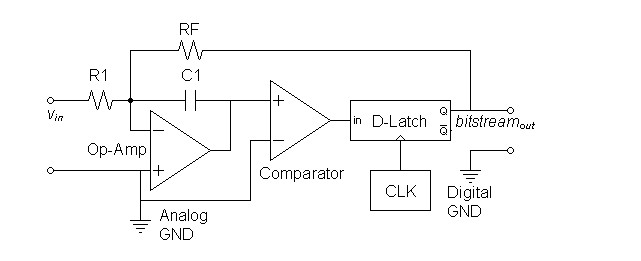Note: Analog ground here represents a reference level at the midpoint of digital output range.

How does this enlighten the process of noise-shaping? Examined simply as an analog system, the modulator has a multiple-feedback arrangement that can be analyzed the same if it were only a simple amplifier. The integrator can be seen viewed as an open-loop block and the application of feedback through R_F determines the overall gain. In this context, the operation of the modulator can be understood in terms of the effect of the feedback. Feedback present in the signal band forces compliance of the output to the input for inband frequencies. At some frequency determined by C₁, R_F, and the apparent gain of the digital block, feedback is released so that digital output swings can occur in out-of-band frequencies. Noise-shaping then is the way that the feedback curve shapes the distribution of the of the out-of-band noise spectrum pertaining to the digital switching activity. The noise spectrum will take the shape of the inverse of the feedback-factor scaled to represent the total out-of-band noise to be represented. In feedback theory terms this is:

(1)

E(s) =

1 + Aβ

where K will vary to scale the total error energy to that output by the modulator

In this case A will represent the integrator gain and β will represent the gain setting feedback factor imposed by R_F. Thus

(2)

E(s) =

1 + (ω_int/s)(R_F/R₁)

Merging scale factors in the denominator the result is:

(3)

E(s) =

1 + ω_system/s

After manipulating to a standard form, it is seen that the noise distribution function is a high-pass function complementary to the lowpass function expected to define the in-band response.

(4)

E(s) = K

s + ω_system

Of course this spectrum is limited on the upper end by the modulation clock frequency.

Figure 4: Signal and modulation noise spectrums of first order modulator.with signal to noise crossover frequency of 100kHz and modulation clock of 2.8MHz.

Legend:
Green: Signal magnitude response.
Red: Modulation noise spectrum.
Neither to scale in magnitude.

Higher-order Modulators

From the bode plot in figure 4 above, it may appear that a first-order modulator may not satisfy high-fidelity audio design requirements. Because the first-order transition from signal band to noise band is slow, feedback that would reduce distortion and quantization noise in the upper audio frequencies is low. Distortion performance is improved by increasing the slope of the transition and therefore the order of the modulator. Digital modulators go as high as the seventh order because digital techniques can achieve high orders with minimal phase shift. Analog techniques generally run into phase shift limitations that limit the slope of the transition. The second-order modulator of figure 5 below is as advanced as reasonable without using some more exotic technology.

Figure 5: Second-order analog modulator

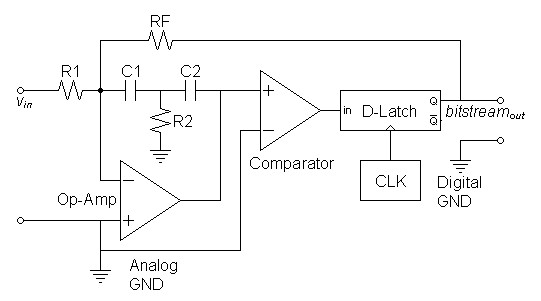Note: Analog ground here represents a reference level at the midpoint of digital output range.

The design of the second order modulator is complicated by excessive phase shift in the second-order integrator. Figure 6 below shows that the integrator has a second-order slope slope up to a frequency where a zero restores a single order slope. Because phase shift in the double slope section can approach 180º compared to 90º for the single slope section, the integrator can be unstable unless the global feedback is greater than the integrator feedback at those frequencies. Therefore the release of feedback to allow the transition from the signal band to the noise band must occur above the zero frequency, shown in figure 6 as 50kHz. If this transition frequency is not high enough above the zero a undesirable resonant peak will occur. The lower the frequency at which the transition occurs the higher the system Q will be and the higher the transition frequency the lower the final system Q. If set up properly, the double slope in the signal band will greatly increase the feedback resulting in lower distortion.

Figure 6: Bode plot of representative second-order integrator response

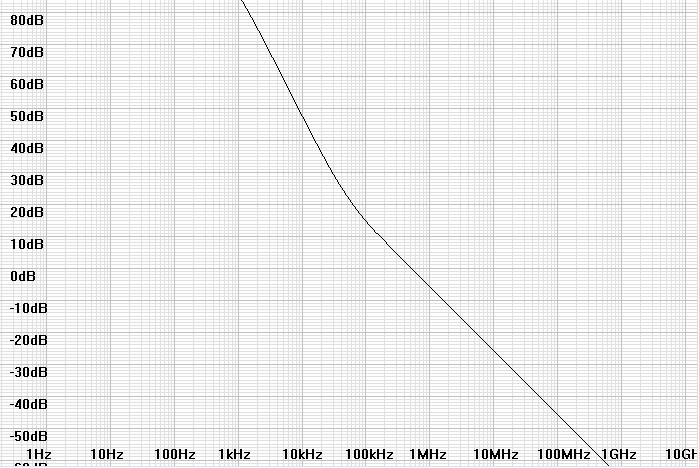The modulator in figure 7 below seems to take the analog modulator as far as it will go. Instead of taking feedback from the output of one D-type flip-flop this circuit puts an analog FIR filter in the feedback path. The shift-register of D₀-D_N creates the series of past signal samples ordinarily needed for a digital filter and the corresponding resistors sum to create the filter function. Because a FIR filter can create a sharp cutoff with little or no phase shift, the gain of the integrator can be raised to give much greater distortion suppression than the simpler analog methods above. Because unnecessary delay is undesirable in a feedback loop the filter type would have to associate the greatest filter weight to the tap off of the first flip-flop D₀. If this were a brickwall filter it would have to be the apodizing type to prevent unnecessary loop delay. Analog FIR filters of this type make excellent DSD filters and are used in many DACs like the PCM1794 to filter DSD streams. Functionally, as lowpass filters, they change the DSD stream containing the embedded analog signal to a PAM signal at the same clock frequency more closely resembling the analog result with no additional magnitude quantization.

Figure 7: High-order analog modulator

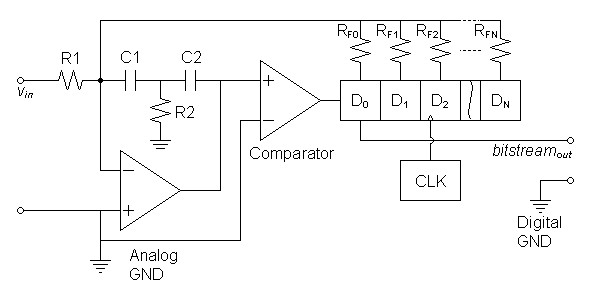Notes:

Filter taps representing negative filter weights will have inverters between the shift-register cell and its corresponding resistor or off any inverting output the cell itself may have..
Analog ground here represents a reference level at the midpoint of digital output range.

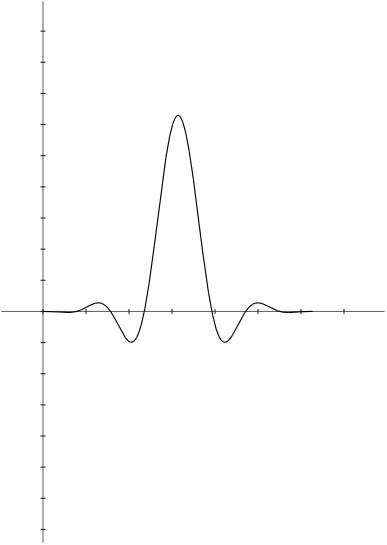
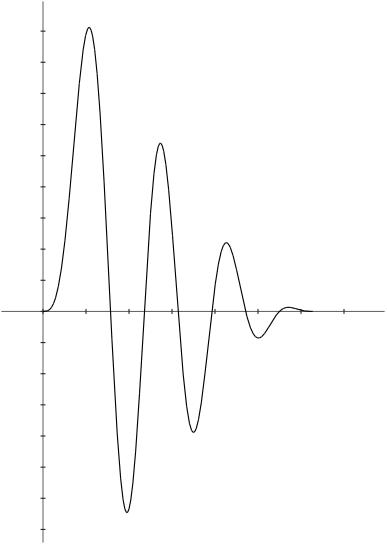
Figures 8 and 9: Illustration of delay issues in the design of the analog FIR filter used in the modulator of figure 7 above.
a – Brickwall filter delays signal by half of kernel time.	b – Apodizing filter moves center of kernel more toward the beginning.

Applications

ADC front ends
DAC back ends
DSD creation
Class-D amplifiers

Document History
January 15, 2013 Created.
January 16, 2013 Corrected some grammar and added an extra phrase of text and graphs of analog FIR filter kernels.