Home  │ Audio Home Page

Copyright © 2012 by Wayne Stegall
Updated November 3, 2012.  See Document History at end for details.

Warp Filter

Introduction

With 60dB or more of DC gain, a phono preamplifier can amplify record warps into subsonic energy dangerous to woofers.  Because of this some proposed long ago to amend the RIAA equalization curve to add a 20Hz highpass pole to filter out subsonics.  However this first-order pole will only suppress warp energy by -31.1261dB.  The filter circuit proposed here has a second-order pole and a notch at the offending frequency to nearly eliminate the problem altogether.

First try

Figure 1:  Desired warp filter topology

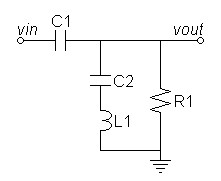Refer to the frequency plot of figure 3 below for the following description.  The circuit of figure 1 above operates in the following manner.  In the passband above 20Hz C₁ passes all signals unaltered.  As the frequency drops to near the cutoff  frequency, L₁ interacts with C₁ and R₁ to create the usual second-order highpass pole at 15Hz.  At this point C₂, because of its larger value, only couples L₁ with the rest of the circuit.  As the response falls due the pole the impedance of c rises as the zero approaches to begin the greater suppression of the notch.  When the impedance of C₂ becomes equal to that of L₁ their opposite polarity results in zero impedance producing the zero magnitude of the notch.  Passing the notch the impedance of C₂ exceeds that of L₁ allowing the magnitude to return to a lower stopband ripple level after which the response drops again in the normal way.

Direct s-domain analysis of circuit produces a third-order transfer curve that does not readily lend itself to a solution.

An empirical solution

It is more desirable then to break the problem down into two parts.  If you can assume that C₂ >> C₁, then C₂ can be removed from the pole analysis allowing separate calculation of pole and zero.  Then the problem reduces to two parts:

• Design circuit with C₂ removed for desired pole.
• Calculate C₂ to give desired zero.
• Simulate and make adjustments if necessary.

Design for pole parameters

Figure 2:  Circuit for pole design

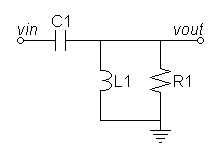First setup and reduce s-domain transfer equation for the simplified circuit:

(1)		sL || R		sLR sL + R
	H(s) =		=
		1 sC1 + sL || R		1 sC1 + sLR sL + R

(2)		sLR		sLR
	H(s) =		=
		sL + R sC1 + sLR		sL + R + s2LC1R sC1

(3)

H(s) =

s2LC1R s2LC1R + sL + R

(4)		s2
	H(s) =
		s2 + s 1 C1R  + 1 LC1

Now the fully reduced transfer equation of equation 4 is in the form of the standard second-order highpass transfer curve.

(5)		s2
	H(s) =
		s2 + s ω Q  + ω2

where the characteristic parameters are derived as follows.

(6)		1
	ω =
		LC1

(7)

Q ω

= C1R,  therefore Q = ωC1R

Combining equations 6 and 7 gives:

(8)		C1R
	Q =
		LC1

Which reduces to:

(9)

Q = R

C1 L

Desiring a Bessel Q, I determined that f_pole for a cutoff of 20Hz is slightly above 15Hz.
Choose 15Hz for pole frequency, then calculate the radian frequency.

(10)	ωpole = 15Hz × 2π = 94.2478 radians/s

The second-order Bessel Q is known as:

(11)		1
	Second order Bessel Q =		≈ 0.57735
		3

Choose R = 100kΩ
Rearrange equation 7 to solve for C₁.

(12)

C1 =

Q ωpoleR

=

0.57735 94.2478 × 100kΩ

= 61.2588nF

Round up to nearest 5% value
C₁ = 62nF

Rearrange equation 6 to solve for L:

(13)

L =

1 ωpole2C1

=

1 (94.2478)2 × 62nF

= 1.81579kH

This huge inductance value will require an active inductor design at a later stage.

Design for zero parameters

Calculate the zero required to cancel a 33⅓  RPM warp:

(14)

fzero =

33.3333 cycles/min 60 s/min

= 0.555555Hz, therefore ωzero = 2π × 0.555555Hz = 3.49066 radians/s

An equation like equation 6 defines the notch frequency relative to L and C₂.  Rearrange it and calculate C₂.

(15)

C2 =

1 ωzero2L

=

1 (3.49066)2 × 1.81579kH

= 45.198µF

Round up to nearest 5% value
C₂ = 47µF
At this point our initial assumption that C₂ >> C₁ is correct, validating this shortcut design method.

The necessity to round C₂ to the nearest standard value requires recalculation of exact L.

(16)

L =

1 ωzero2C2

=

1 (3.49066)2 × 47µF

= 1.74617kH

SPICE results

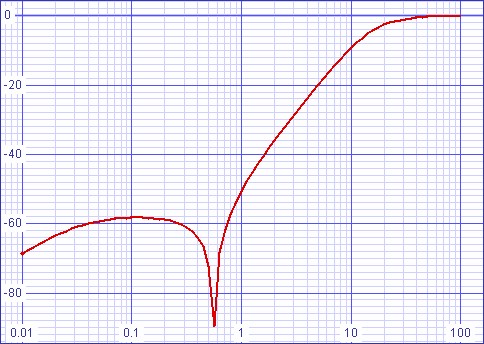
SPICE results verify successful design outcome.

SPICE model.

Figure 3:  Passive filter magnitude response	Figure 4:  Passive filter phase response
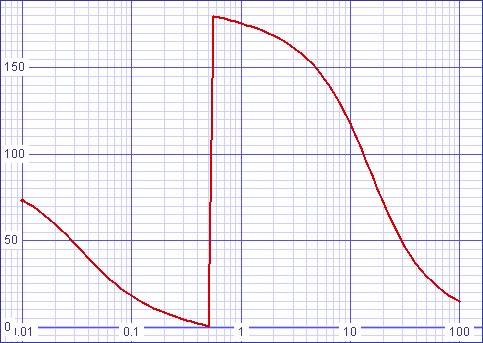Figure 5:  Passive filter magnitude notch detail 0.5-0.75Hz

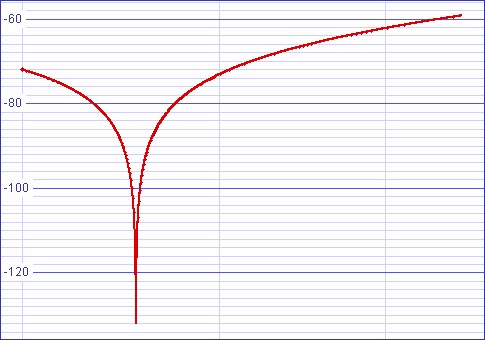Magnitude response at 0.555555Hz (33⅓  RPM warp) = -165.432dB
Magnitude response at 0.75Hz (45  RPM warp) = -59.288dB
Magnitude response at 20Hz = -2.59905dB.

I did not simulate distortion because it depends on final component choice.

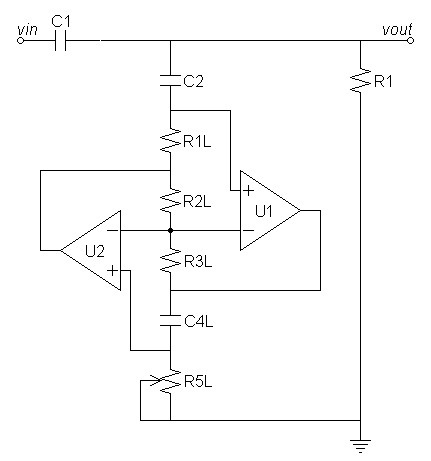
Add active inductor to design

The circuit that follows in figure 5 adds an active inductor consisting of U₁, U₂, R_1L, R_2L, R_3L, C_4L, and R_5L.  It is a form of a circuit known as a  Generalized Impedance Converter.  Concerns by those who prefer discrete circuits to operational amplifiers are mitigated by the fact that the active inductor is only in the signal path in the passband near the resonant frequency.

Figure 6:  Warp filter with active inductor

The equivalent active inductance is calculated by the formula:

(17)

L =

C4L × R1L × R3L × R5L R2L

I choose C_4L to be 1µF because it is the largest among plastic capacitors to be of reasonable size and price.  Then I presume that the resistors would give the best noise result if they were the same values.  If all the resistors were set the same in equation 17 above then equation 17 above simplifies to:

(18)

L =

C4L × R1L × R1L × R1L R1L

= C4L × R1L2

Rearrange equation 18 and solve for common resistor value.

(19)

R1L =

L C4L

=

1.74617kH 1µF

= 41.7872kΩ

Round to the nearest 1% value.
R_1L, R_2L and R_3L = 42.2kΩ

Now restore R_5L to equation 18 to calculate its similar adjustable value.

(20)

L =

C4L × R1L × R1L × R5L R1L

= C4L × R1L × R5L

Rearrange equation 20 and solve for R_5L.

(21)

R5L =

L C4L × R1L

=

1.74617kH 1µF × 42.2kΩ

= 41.3784kΩ

SPICE results

Again SPICE results confirm a successful design outcome.

SPICE model with active inductor.

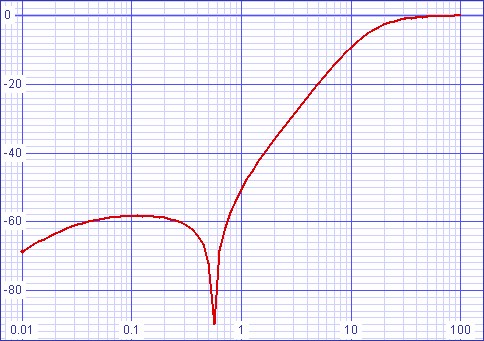
Figure 7:  Passive/active filter magnitude response	Figure 8:  Passive/active filter phase response
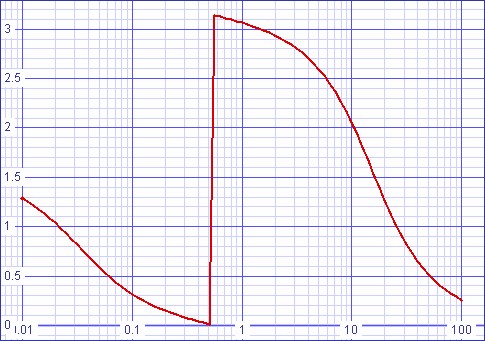Figure 9:  Passive/active filter magnitude notch detail 0.5-0.75Hz

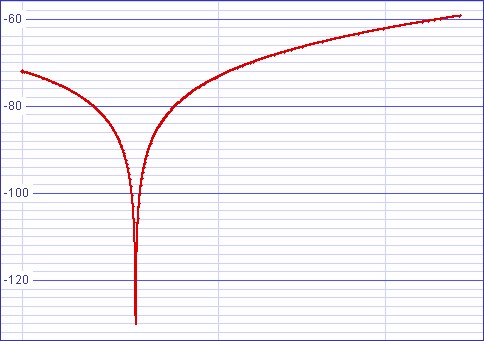Magnitude response at 0.555555Hz (33⅓  RPM warp) = -134.583dB
Magnitude response at 0.75Hz (45  RPM warp) = -59.2881dB
Magnitude response at 20Hz = -2.59943dB.

Because the GIC is supposedly a proven circuit, I used ideal op amps in the simulation.

Application and Adjustments

In actual application, the proper operation of this passive circuit is sensitive to the circuit context into which it is placed.  Therefore a buffer should drive it with near zero output impedance and the output should drive near infinite input impedance in the buffer that follows.

Adjust R_5L to calibrate the correct notch frequency in the manner you see best.  I would suspect you would play a warped record at 33⅓  RPM and then

• Measure C₂ with an LCR meter and with same meter set l to the exact value necessary.  Depending on the exact C₂ value, you may have to recalculate L again as in the equations above.
  
• Connect an oscilloscope and adjust for the best null or
• Play it carefully through loudspeakers always monitoring for safe volume until the woofer no longer responds to the warp signal.

Generalized Impedance Converter (GIC)

For those curious about the active inductor itself, I include a little information about the basis circuit itself.¹

Figure 10:  GIC can emulate many other impedances other than the active inductor

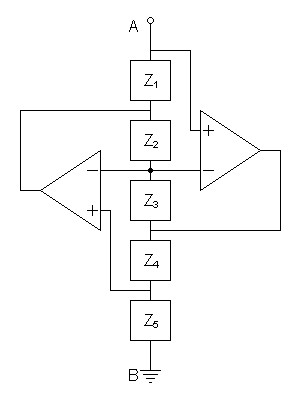Node B is always shown in the source document connected to ground.  There is no logical reason to think it has to be this way.

The virtual impedance created by the circuit of figure 10 above is:

(22)

ZGIC =

Z1Z3Z5 Z2Z4

¹Arthur B. Williams and Fred J. Taylor, Electronic Filter Design Handbook (New York, 1988), p. 3-39 - 3-41 "Generalized Impedance Converters."

Document History
September 22, 2012  Created.
September 23, 2012  Made a minor correction just prior to equation 15.
September 25, 2012  Corrected misspellings.  I moved quickly to publish but I thought I did a spell check.
November 3, 2012  Corrected some grammer.