Thermal Design

Part 1:
Thermal design for gainclone and one-bend amplifiers is used to illustrate the presented theory.

Introduction

For the purposes of managing heat in electronic devices, thermal elements are considered to have a thermal resistance equal to the temperature difference between the two ends of the element divided by the associated flow of heat power. The relation is mathematically equivalent to Ohm's law and therefore allows represent ion and solution of the thermal system as is if it were a resistor network.

(1)

Thermal Resistance (ºC/W) =

Temperature (ºC)

Heat Flow (W)

Here heat itself would be in units of Joules (J), however the flow of heat would represent power in Watts.

Class B Thermal Design

Calculation of Power Dissipation

Before a thermal design can be done the power dissipated by all the devices feeding into the design heat sink must be calculated.

First calculate average output power. Output power is related to rms output voltage and is calculated from peak voltage with a scale factor of ½.

(2)

P_OUT =

V_OUT-PEAK²

2R_L

Note: It is more desirable to relate power to peak-voltage here because the peak output voltage is related to the supply voltage by the dropout voltage if it is not limited by some other factor as well.

(3)

V_OUT-PEAK ≤ V_CC – V_DO

Here V_DO represents the inability of an amplifier to drive its output voltage all the way to the supply voltage.

Now calculate input power. Because the supply voltages are considered constant, the average power is proportional to the average current. Only the voltage of a single supply is used because apart from a small amount of bias a class b output stage only draws power from one rail of the power supply at a time.

(4)	P_IN = V_CC × I_OUT-AVE

Average current is scaled from peak current by a scale factor of 2/π (≈63.7%).

(5)

P_IN = V_CC

I_OUT-PEAK

It may be easier to calculate input power from all voltages.

(6)

P_IN =

V_CC × V_OUT-PEAK

R_L

You may want to calculate the efficiency as well.

(7)

Eff =

P_OUT

P_IN

	V_OUT-PEAK² 2R_L

	2V_CC × V_OUT-PEAK πR_L

(8)

Eff =

V_OUT-PEAK

V_CC

Note here that a maximum efficiency of π/4 (≈78.5%) is only attainable if the output can be driven all the way to supply voltage.

Finally power dissipation is just input power minus output power.

(9)

P_DISS = P_IN – P_OUT =

2V_CC × V_OUT-PEAK

πR_L

–

V_OUT-PEAK²

2R_L

(10)

P_DISS =

4V_CC × V_OUT-PEAK – V_OUT-PEAK²

2πR_L

Example

Having no class B amplifier design on hand, it seems useful to do the thermal design of the popular gainclone. The relevant specifications of the popular LM3886 chip for optimal drive into a 4Ω load are:

V_CC		28V		P_OUT		68W
T_J-MAX		150ºC		R_θJC		1ºC/W

Even though not a device parameter itself, the text of the datasheet suggested the thermal resistance of a mica insulator and thermal compound combination as:
R_θCS = 0.2ºC/W

Given output power, calculate peak output voltage to prepare remaining calculations.

(11)

V_OUT-PEAK =

2P_OUTR_L

2 × 68W × 4Ω

= 23.3238V

Calculate input power.

(12)

P_IN =

V_CC × V_OUT-PEAK

R_L

28V × 23.3238V

4Ω

= 103.939W

Finally calculate the power dissipation.

(13)	P_DISS = P_IN – P_OUT = 103.939W - 68W = 35.9387W

Figure 1: Thermal circuit representing one semiconductor device mounted to a heat sink

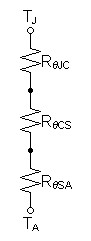For an ambient temperature of 25ºC calculate thermal resistance of desired heat sink.

(14)	T_J – T_A = P_DISSR_θJC + P_DISSR_θCS + P_DISSR_θSA

(15)	R_θSA =	T_J – T_A – P_DISS(R_θJC + R_θCS) P_DISS

(16)	R_θSA =	150ºC – 25ºC – 35.9387W(1ºC/W + 0.2ºC/W) 35.9387W

(17)	R_θSA =	2.27814ºC/W

Perhaps a presumption of an ambient temperature of 25ºC is too optimistic, try 50ºC (>120ºF).

(18)	R_θSA =	150ºC – 50ºC – 35.9387W(1ºC/W + 0.2ºC/W) 35.9387W

(19)	R_θSA =	1.58252ºC/W

SPICE Analysis

SPICE model

Figure 2: SPICE model of thermal circuit of figure 1

* Thermal circuit for LM3886 gainclone
* SPICE version: Spice Opus 2.31
i1 0 tj dc 35.9387
rthjc tj tc 1
rthcs tc ts 0.2
rthsa ts ta 1.58252
v1 ta 0 dc 25
.end
.control
op
print all
.endc

Figure 3: SPICE output for model of figure 2.

      ta = 2.500000e+001
      tc = 8.906145e+001
tj = 1.250002e+002
ts = 8.187371e+001
v1#branch =
3.593870e+001

    

Class A Thermal Design

Calculation of Power Dissipation

Output power is always calculated the same Therefore the same equation is used here as in the class b calculations

(2)

P_OUT =

V_OUT-PEAK²

2R_L

Because transistors operated in class a never turn off the average supply current is always the same as the operating bias current. Unlike with class b input power is independent of output power.

(20)	P_IN = 2V_CC × I_BIAS

It may be useful to calculate input power in terms of voltage rather than bias current.

(21)

If I_BIAS =

V_OUT-PEAK

2R_L-MIN

(22)

P_IN =

V_CC × V_OUT-PEAK

R_L-MIN

Again efficiency calculations may be of interest.

(23)

Eff =

P_OUT

P_IN

	V_OUT-PEAK² 2R_L

	V_CC × V_OUT-PEAK R_L-MIN

(24)

Eff =

V_OUT-PEAK × R_L-MIN

2V_CC × R_L

As always the transistors dissipate the input power that does not go to the output.

(25)	P_DISS = P_IN – P_OUT

Therefore, a constant input power produces a condition where the transistors dissipate maximum power at a zero output level.

(26)	P_DISS-MAX = P_IN

and minimum power when the output is at its maximum.

(27)	P_DISS-MIN = P_IN – P_OUT-MAX

Example

It seemed that a proper thermal design was a necessary prerequisite to adding a safe-area limiter to the one-bend amp. Although the project was originally conceived only to investigate how to design the transfer curve of an amplifier, I feel compelled to make every aspect of the design correct as time permits.

To begin, the IRFP240 and IRFP9240 datasheets give the following thermal data

P_D		150W @ T_C = 25ºC		T_J		–55ºC – 150ºC
R_θJC		0.83ºC/W		R_θCS		0.24ºC/W, flat surface with thermal grease

First calculate input power.

(28)	P_IN = 2V_CC × I_BIAS

(29)	P_IN = 2 × 35V × 4A

(30)	P_IN = 280W

Since the transistors have to dissipate all of the input power at idle, the power calculations are complete.

(31)

P_DISS = P_IN = 280W

Now calculate for a heat sink protecting four output transistors as in figure 4.

Figure 4: Thermal circuit representing four semiconductor devices mounted to a heat sink

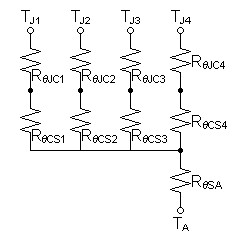First calculate power dissipation required of each transistor.

(32)	P_DISS/DEVICE = P_IN/#devices

(33)	P_DISS/DEVICE = 280W/4 devices

(34)	P_DISS/DEVICE = 70W

Now setup and solve thermal circuit equations for heat sink thermal resistance.

(35)	T_J – T_A = P_DISS/DEVICER_θJC1 + P_DISS/DEVICER_θCS1 + (#devices × P_DISS/DEVICE)R_θSA

(36)	R_θSA =	T_J – T_A – P_DISS/DEVICE(R_θJC1 + R_θCS1) #devices × P_DISS/DEVICE

(37)	R_θSA =	150ºC – 50ºC – 70W × (0.83ºC/W + 0.24ºC/W) 4 × 70W

(38)	R_θSA =	0.0896429ºC/W

In spite of the fact that four output devices appeared to be able dissipate 280W on first glance, the required heat sink seems unreasonably large especially considering that you would likely choose a larger one for the reliability of a lower junction temperature.

Now recalculate for eight output devices and an ambient temperature of 50ºC.

Figure 5: Thermal circuit representing eight semiconductor devices mounted to a heat sink

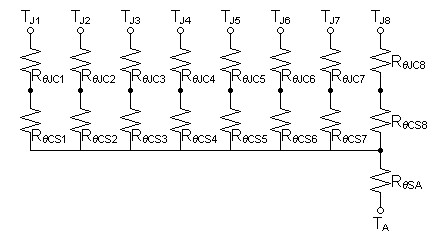First calculate power dissipation required of each transistor.

(39)	P_DISS/DEVICE = P_IN/#devices

(40)	P_DISS/DEVICE = 280W/8 devices

(41)	P_DISS/DEVICE = 35W

Now setup and solve thermal circuit equations for heat sink thermal resistance.

(42)	R_θSA =	T_J – T_A – P_DISS/DEVICE(R_θJC1 + R_θCS) #devices × P_DISS/DEVICE

(43)	R_θSA =	150ºC – 50ºC – 35W × (0.83ºC/W + 0.24ºC/W) 8 × 35W

(44)	R_θSA =	0.223393ºC/W

This heat sink value is reasonable, however 0.1ºC/W heat sinks are available and would lower the transistor junction temperature more.

SPICE Analysis

SPICE model

Figure 6: SPICE model of thermal circuit of figure 5

* Thermal circuit for eight transistor class a output stage.
* SPICE version: Spice Opus 2.31
i1 0 tj1 dc 35
i2 0 tj2 dc 35
i3 0 tj3 dc 35
i4 0 tj4 dc 35
i5 0 tj5 dc 35
i6 0 tj6 dc 35
i7 0 tj7 dc 35
i8 0 tj8 dc 35
rthjc1 tj1 tc1 0.83
rthcs1 tc1 ts 0.24
rthjc2 tj2 tc2 0.83
rthcs2 tc2 ts 0.24
rthjc3 tj3 tc3 0.83
rthcs3 tc3 ts 0.24
rthjc4 tj4 tc4 0.83
rthcs4 tc4 ts 0.24
rthjc5 tj5 tc5 0.83
rthcs5 tc5 ts 0.24
rthjc6 tj6 tc6 0.83
rthcs6 tc6 ts 0.24
rthjc7 tj7 tc7 0.83
rthcs7 tc7 ts 0.24
rthjc8 tj8 tc8 0.83
rthcs8 tc8 ts 0.24
rthsa ts ta 0.223393
v1 ta 0 dc 25
.end
.control
op
print all
.endc

Figure 7: SPICE output for model of figure 6.

      ta = 2.500000e+01

tc1 = 9.595004e+01

tc2 = 9.595004e+01

tc3 = 9.595004e+01

tc4 = 9.595004e+01

tc5 = 9.595004e+01

tc6 = 9.595004e+01

tc7 = 9.595004e+01

tc8 = 9.595004e+01

tj1 = 1.250000e+02

tj2 = 1.250000e+02

tj3 = 1.250000e+02

tj4 = 1.250000e+02

tj5 = 1.250000e+02

tj6 = 1.250000e+02

tj7 = 1.250000e+02

tj8 = 1.250000e+02

ts = 8.755004e+01

v1#branch = 2.800000e+02

Try this yourself. Alter the SPICE model for a 0.1ºC/W heat sink and note the much lower junction temperature.

Document History
July 12, 2013 Created.
July 12, 2013 Corrected R_θSA in SPICE model of figure 6, regenerated corresponding SPICE output, and made minor improvements to wording.
April 20, 2015 Corrected some misspellings.