Room Effect and Speaker Alignment

Introduction

I have long held the opinion that a sealed-box speaker would outperform a ported design on technical merits pertaining to lower phase shift in the deep bass. More recently I began to question whether the phase effects of the room effect would drown out the phase differences of the two vindicating the recent trend toward dominance of ported speakers.

Anechoic response

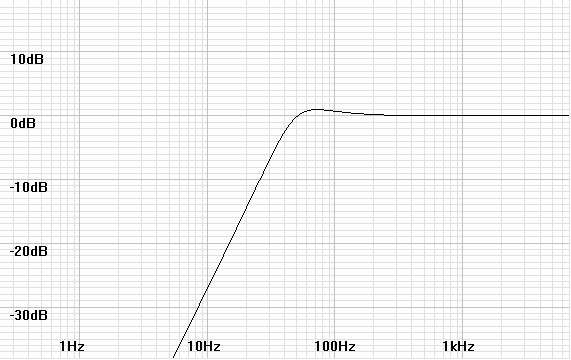
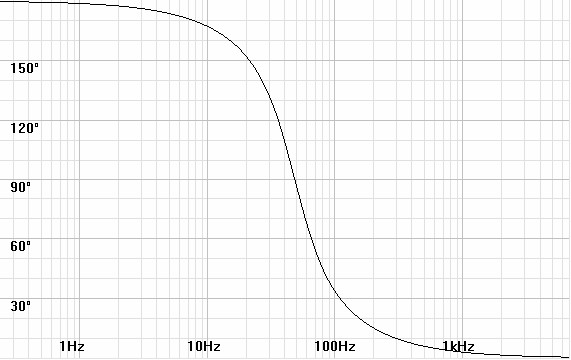
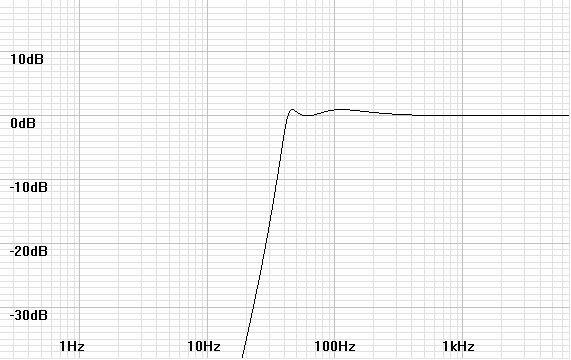
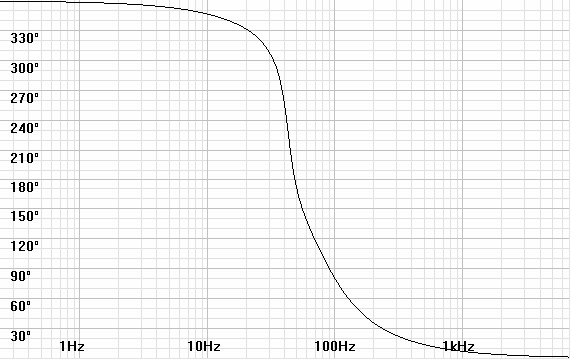
If comparable speakers of each type were analyzed without alteration of the room effect, figures 1-4 below would show the sealed-box speaker a clear winner regarding phase response. Both were calculated for a 40Hz cutoff at -3dB with a 1dB Chebychev alignment. At the 40Hz cutoff the sealed-box phase shift is 109.789º; that for the ported design is 256.208º.

Figures 1 and 2: Bode and phase plots for a sealed box speaker with a 40Hz cutoff and a 1dB ripple Chebychev alignment.

Figures 3 and 4: Bode and phase plots for a ported speaker with a 40Hz cutoff and a 1dB ripple Chebychev alignment.

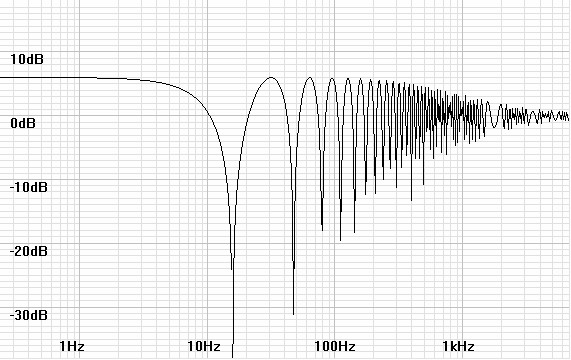
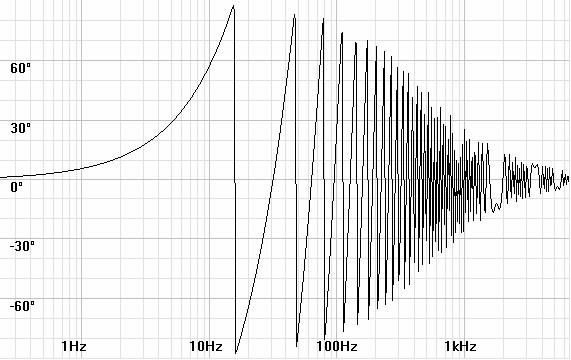
The room effect complicates analysis

Placing the same speakers in an actual live room greatly alters their response because standing waves create resonances at fundamentals and harmonics related to room dimensions. The result of adding a signal back to itself after bouncing off two parallel walls produces a comb filter response where the signal doubles at resonant frequency and its harmonics and cancels at intermediate frequencies while the phase goes from -90 to +90 and then abruptly back repeated at the same interval as the magnitude response. This effect ends as the frequencies rise to where they are absorbed by the room rather than reflecting between the walls, in these plots depicted to occur at 500Hz. (figures 5 and 6)

Note: All room effects shown are worst case: against a reflecting wall for one-dimensional cases and in a corner for three-dimensional ones. Actual responses out into listening room will be better and will vary.

Figures 5 and 6: Bode and phase plots for a hypothetical one-dimensional room effect between two parallel walls spaced 18ft apart.

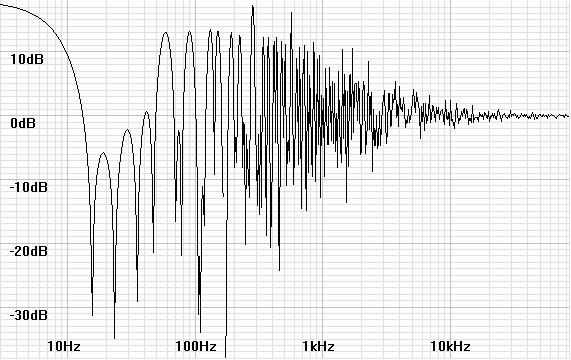
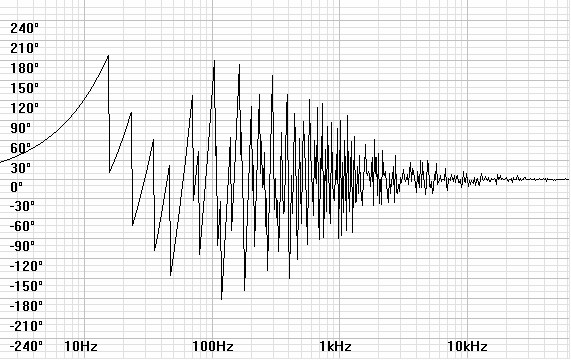
If the room effect along one dimension is bad enough, the effect occurs in three dimensions for most typical box-shaped rooms. The response then is of three comb filters at different fundamental frequencies combining into a more chopped up frequency response as shown in figures 7 and 8 below.

Figures 7 and 8: Bode and phase plots for a hypothetical three-dimensional room effect for a room 18' x 12' x 8'

Speaker response with room effect

The following plots superimpose a one-dimensional room effect on each type of speaker. Even with the ±90º phase variation of the one-dimensional room effect added to the speaker responses there is still a seeming difference favoring the seal-box design. Even if the difference between the two is clouded by room resonance, there may still be a subjectively audible difference to be heard. Also, it is possible that the human auditory system may hear the correct speaker response in spite of the room effect, reading the room effect only as the ambience of the listening space. The use of comb filters to create simulated stereo from mono and the perception of missing fundamentals in small speakers when the second and third harmonics are present seem to support this concept.

Figures 9 and 10: Bode and phase plots for the sealed box speaker with one-dimensional room effect.

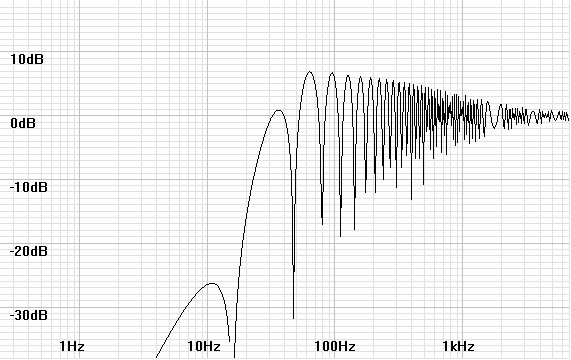
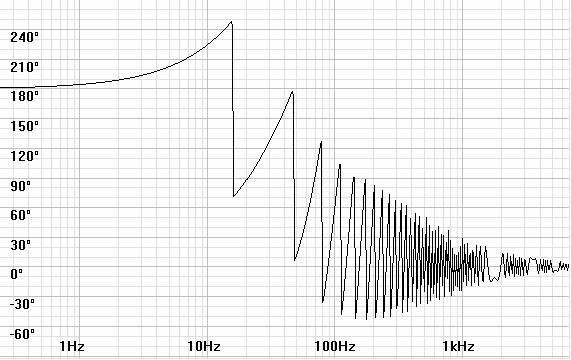
Figures 11 and 12: Bode and phase plots for the ported speaker with one-dimensional room effect.

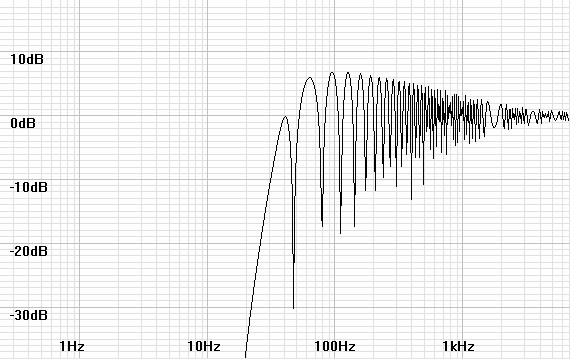
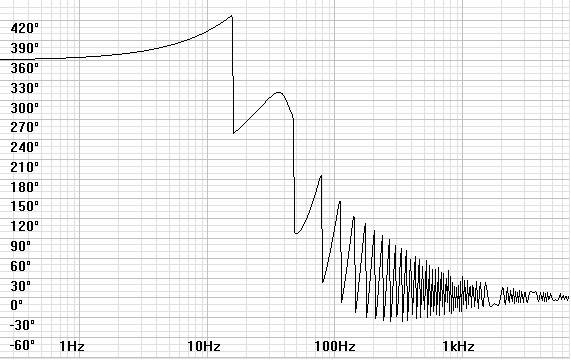
Direct Coupling

An additional room effect that can distinguish the sealed-port speaker from the ported one might be called direct coupling. Allegedly, below the lowest resonance frequency of the room a sealed-port speaker pressurizes the room as a whole instead of creating waves. If the resonance frequency of the speaker is matched to be equal to or lower than that of the room the sealed-box response will not end below its resonance frequency but continue down short of DC. This is the same effect that allows closed-back headphones to have frequency response down to low frequencies in spite of small dimensions that would limit bass response. Direct coupling, however, works against ported speakers. In ported speakers, direct coupling only serves to couple the woofer to its port cancelling signals below the port resonance frequency.

Where length is the longest dimension of room, f₀ is the resonant frequency of the speaker, and c is the velocity of sound in compatible units (1132ft/sec), the following equation related the condition for direct coupling of a sealed-box speaker to a room.

Length ≤

f₀

Figure 5: Sealed-box speaker matched for direct coupling would simply show frequency response of room effect	Figure 11: Not benefiting from direct coupling, the ported speaker would show the predicted combined room-speaker response already plotted.

Personal Note

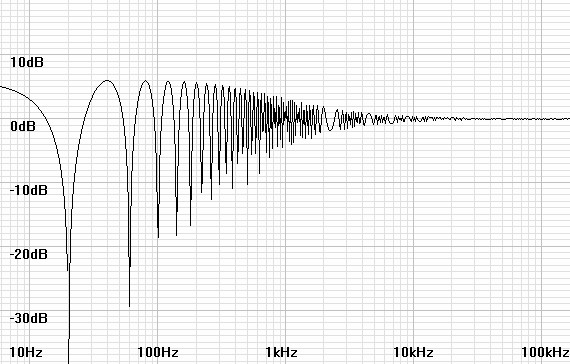
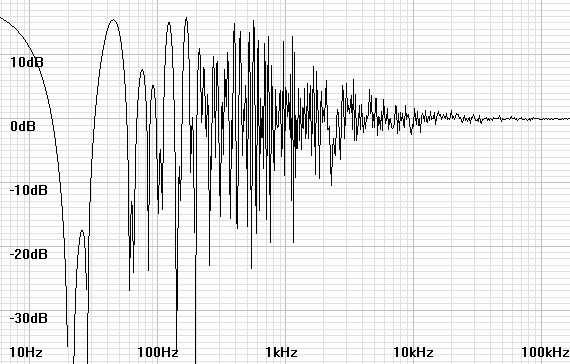
For 17 years I had my sealed-box speakers in a room optimally matched to them for direct coupling and did not know it. Ironically, I was devising how to equalize them to extend down to 20Hz when I likely already had the response I desired. Figures 13 and 14 show the calculated response of room involved and therefore likely also of the speakers in it. The room effect notches would have been unavoidable in any case and been mitigated by listening out into the room rather than at the reverberation boundaries.

Figures 13 and 14: One and three-dimensional room effect plots calculated for the room that I long played my sealed-box speakers.

Document History
December 6, 2013 Created.