Home  │ Audio Home Page

Copyright © 2009 by Wayne Stegall
Updated October 13, 2010.  See Document History at end for details.

Basic Electronics

Power Supply Ripple Calculations and Capacitor Size

Figure 1:  Graph of full-wave rectification with capacitor ripple

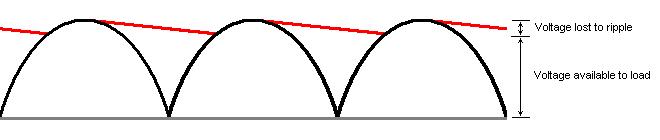The peak voltage from a transformer (1.414 x V_rms) has to be derated by the ripple voltage and diode drop before furthur power supply calculations can be done.  Ripple calculations are derived from the capacitor formula.  Because this formula is common and important, it may be better to remember the capacitor formula

Begin with the capacitor formula (current = capacitance x rate of change of voltage)

(1)

i = C

δv δt

Change instantaneous slope (δv/δt) to constant slope over finite interval (Δv/Δt) and solve it for voltage change.

(2)

Δv =

iΔt C

Where Δv is ripple voltage, i is load current, Δt is ripple interval (1/120 s for full wave rectification and 1/60 s for  half wave at 60Hz line frequency), and C is capacitance.

It may be more convenient to relate Δt as frequency instead.  Substitute 1/f for Δt in equation (2).

(3)

Δv =

i fC

Now f represents ripple frequency (120Hz for full wave rectification and 60Hz for half wave rectification)


Example:
Given full wave rectification, a load current of 3.5A, and a capacitance of 6800µF, calculate the ripple voltage.

From equation (3)

Δv =

3.5A 120Hz x 6800µF

=  4.29V

As for the thought that lead to this article.  Reading that 47 Labs used 1000µF in its Gaincard amplifier power supplies puzzled me.  Do more powerful amplifiers require larger capacitors?  On first impression it seems so.  However, lets rearrange our ripple equation again.

(4)

Δv i

=

1 fC

Δv/i is in the form of a resistance.  Ripple voltage increases with output current just like a voltage drop due to an output impedance would.  The limitation on the useful output of the raw power supply could be modeled as an equivalent output resistance.  This would not be a real model but an abstraction to aid viewing the concept in a useful way.  It would be clear then that the percent ripple would be the same into a constant load (as the 4 to 8Ω of an audio amplifier load) regardless of the supply voltage (and therefore maximum power).  In cases where a low feedback factor in the amplifier causes concern regarding hum, a fixed ripple calculation would still be more valid.

Figure 2:  Schematic of ripple abstraction

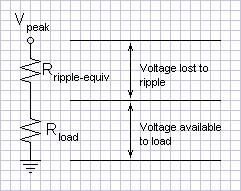The equivalent output impedance with the above mentioned 1000µF filter capacitors is:

From equation (4)

Δv i

=

1 120Hz x 1000µF

= 8.33Ω

You can immediately imagine a voltage divider with respect to an 8Ω load that would give more ripple than maximum voltage signal.  In this case the designer sacrificed a great deal of power to get something else in return.  All capacitors have stray inductance that compromises their high frequency regulation ability.  (They actually act more like inductors above their resonant frequency, f = 1/(2πsqrt(LC)))  The factors involved in increasing capacitance increase this stray inductance as well (at least in the construction of electrolytic capacitors).  Power supply speed is the quest of this engineer.  In theory, stray inductance could be minimized in conjunction with a large capacitance by paralleling smaller capacitors because paralleling reduces inductance while increasing capacitance (You can verify the math.).  It is convenient to this end that low-esr capacitors tend to be found in smaller values.  Paralleling small capacitors having better high frequency regulation with electrolytics is also a common practice.

What of the answer to the question posed?¹  Capacitor size does not need to increase with the size of the amplifier unless insufficient amplifier feedback factor (or insufficient regulation in the case of regulated power supplies) makes power supply hum a real issue.


¹Deliberate use of sentence fragment per Birk, Newman P. and Genevieve B., Understanding and Using English (1972), p. 405, "Some grammatically incomplete sentences convey clearly and appropriately the meaning the communicator wishes to say"

Document History
December 6, 2009 created.
October 13, 2010  Corrected grammer of one sentence.