Digital Phono Equalization

Introduction

Some may want to equalize their vinyl digitally for some reason. For one, some modern preamps are all digital, requiring digital equalization. Others, wanting to record their LPs to their computer, attribute some benefit to equalizing their collection without the sonic defects attributed to circuits with analog capacitors. I attempt here to address the latter interest mainly, although it has application to the former as well.

Some concise theory

Most are accustomed to representations of filter function in Laplace terms in the s-domain. However, digital filters are native to another domain known as the z-domain. Fortunately, the two are related and ideas in one can be translated to the other.

In this case we expect RIAA equalization to be represented by

(1)

H(s) =

(s – z₁)

(s – p₁)(s – p₂)

where z₁ ,p₁, and p₂ represent turnover frequencies defined as

(2)

ω = 2πf₀

To transform our equation to the z-domain required for digital analysis every element in H(s) is transformed by

(3)

z = e^sT, where T =

f_s

the inverse of the samplingfrequency.

In particular new poles and zeros are calculated

(4)	p(z) = e^p(s)T, where p(s) is in natural frequency ω = 2πf₀

In full the calculation is

(5)

p(z) = e

2πf₀

f_s

The transformed response equation has a similar appearance

(6)

H(z) =

z – z₁

(z – p₁)(z – p₂)

In order to obtain filter coefficients the separate pole and zero factors must be multiplied out to a full polynomial in the numerator and denominator.

(7)

H(z) =

z – z₁

z² + (– p₁– p₂)z + p₁p₂

Once normalized and adjusted for gain, the filter coefficients emerge.

(8)

H(z) =

b₀ + b₁z^-1

1 + a₁z^-1 + a₂z^-2

If it appears that I have careless in factoring multiplying or dividing out entire factors of z, z or z^-1 alone as a factor only represents advance or delay of T length time periods respectively.

When the frequency and phase response are to be evaluated, Euler's law puts all frequencies on a unit circle where frequency is represented by the angle.

(9)	e^jωT = cos(ωT) + sin(ωT)j

For convenience frequencies are often made relative to the sampling frequency.

(10)

ω_z = ωT =

f_s

(11)

f_z = fT =

f_s

Then the upper frequency limit of ½f_s limits z-domain frequencies to the ranges –π < ω < π and -0.5 < f < 0.5.

IIR vs FIR

There are two major types of digital filters, FIR and IIR, that is finite impulse response and infinite impulse response respectively. Only the IIR filter is a direct equivalent to an analog filter because only it has the poles that every analog filter must possess. Equalization can be done with a FIR filter which has all zeros. However, the FIR filter would have many zeros that only imperfectly duplicated the poles. You can illustrate this by doing long division on the IIR equation. The resulting infinite zeros of the resulting FIR filter would then have to be truncated to enable finite computations resulting in frequency ripple that the IIR filter would not have. Be sure too the the FIR filter was not linear phase or the equalization would not be phase correct. Because of this the design that proceeds is an IIR design.

Numerical calculations

The fact that sampling frequency enters calculation of poles and zeros means that different filter coefficients have to be calculated for every combination of sampling frequency and gain. Therefore a computer program such as in figure 1 below is useful to calculate the desired filter. In Linux – and maybe OS X as well – just paste the program in to a file named riaaiir.c and execute the gcc compiler.

gcc riaaiir.c -lm -o riaaiir

Make it executable.

chmod +x riaaiir

Then execute it.

./riaaiir

Figure 1: riaaiir.c program listing

      
#include <stdio.h>

#include <string.h>

#include <math.h>

typedef struct {int nn, nd; double n[3], d[3];} biquad;

#define TP1 3180e-6

#define TP2 75e-6

#define TZ1 318e-6

#define TZ2 3.18e-6

#define PZ(T) exp(-1.0/(fs*(T)))

biquad computeriaaiir(double fs, double dcgain, int extrazero)

{

  static biquad bq;

  double p1, p2, z1, z2, gain;

  int i;

  p1 = PZ(TP1);

  p2 = PZ(TP2);

  z1 = PZ(TZ1);

  z2 = PZ(TZ2);

  bq.nd = 3;

  bq.d[0] = 1.0;

  bq.d[1] = -p1-p2;

  bq.d[2] = p1*p2;

  if(extrazero)

  {

    bq.nn = 3;

    bq.n[0] = 1.0;

    bq.n[1] = -z1-z2;

    bq.n[2] = z1*z2;

  }

  else

  {

    bq.nn = 2;

    bq.n[0] = 1.0;

    bq.n[1] = -z1;

    bq.n[2] = 0.0;

  }

  gain = (bq.n[0]+bq.n[1]+bq.n[2])/(1.0+bq.d[1]+bq.d[2]);

  for(i=0; i<3; i++)

    bq.n[i] *= (dcgain/gain);

  return bq;

}

void printbiquadcoeff(biquad bq)

{

  int i;

  printf("Coefficients for H(z):\n\n");

  printf("num");

  for(i=0; i<bq.nn; i++)

  {

    printf("[%1d] = %e",i,bq.n[i]);

    if(i<bq.nn-1)

      printf(", ");

  }

  printf("\n--------------------------------"\

    "--------------------------------\n");

  printf("den");

  for(i=0; i<bq.nd; i++)

  {

    printf("[%1d] = %e",i,bq.d[i]);

    if(i<bq.nd-1)

      printf(", ");

  }

  printf("\n\n");

  printf("Audacity Nyquist biquad equations (LISP format)\n");

  // a's are denominators

  printf("(biquad s b0 b1 b2 a0 a1 a2)\n");

  printf("(biquad s");

  for(i=0; i<3; i++)

    printf(" %e",bq.n[i]);

  printf(" 1.0");

  for(i=1; i<3; i++)

    printf(" %e",-bq.d[i]);

  printf(")\n");

  printf("(biquad-m s b0 b1 b2 a0 a1 a2)\n");

  printf("(biquad-m s");

  for(i=0; i<3; i++)

    printf(" %e",bq.n[i]);

  for(i=0; i<3; i++)

    printf(" %e",bq.d[i]);

  printf(")\n\n");

}

int main()

{

  biquad riaa;

  double fs, gain;

  int extrazero;

  do

    printf("\nEnter sampling frequency, dc gain, and 0/1
for extra zero:  ");

  while(3 < scanf("%lf%lf%d",&fs,&gain,&extrazero));

  printf("\n");

  riaa = computeriaaiir(fs,gain,extrazero);

  printbiquadcoeff(riaa);

  printf("\n");

  return 0;

}

Click here to download Windows version of the program.

Simulating the filter

After the calculated coefficients are applied to the equation for H(z), that equation can be used to plot the expected frequency and phase responses. Figure 2 below shows a plot of the RIAA filter calculated at the CD audio sampling rate.

Figure 2: Plot of H(z) for coefficients calculated for 44.1kHz.

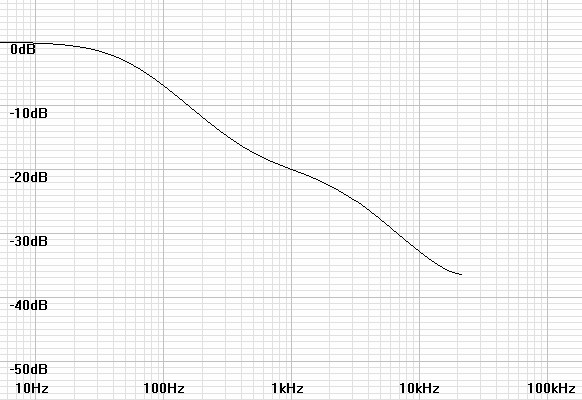Notice in this plot that near the frequency limit at ½f_s the response turns back up as if an extra zero near that frequency were applied. This is a recognized anomaly. I suspect that phase compression that locks all phases to 0º or 180º – whichever is nearer – forces an analog response approaching ½f_s that is consistent with the compelled phase: thus the appearance of an added pole. The solution seems to be to raise f_s until the anomaly does not affect the audio band. The following plots of filters calculated at higher sampling frequencies illustrate the latter conclusion.

Figure 3: Plot of H(z) for coefficients calculated for 96kHz.

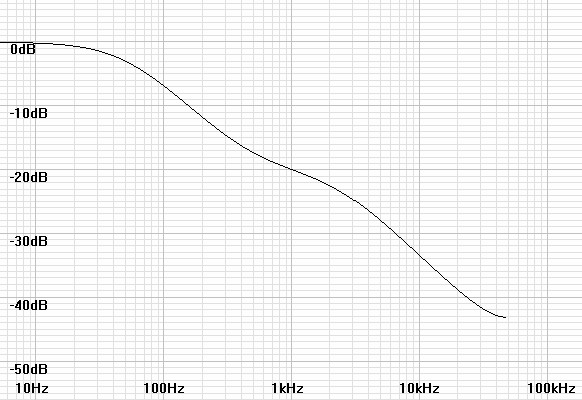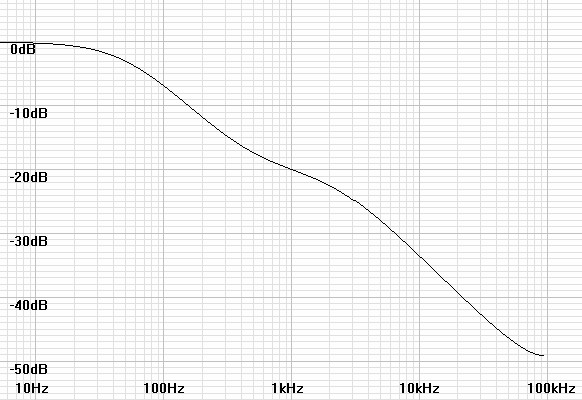
Figure 4: Plot of H(z) for coefficients calculated for 192kHz.

The filter plots alone do not show exactly how the frequency response is affected by the anomaly. Therefore the following plots add the filter response to that of an analog inverse RIAA filter to predict the actual final response.

Figure 5: Plot of H(z) for coefficients calculated for 44.1kHz with inverse RIAA.

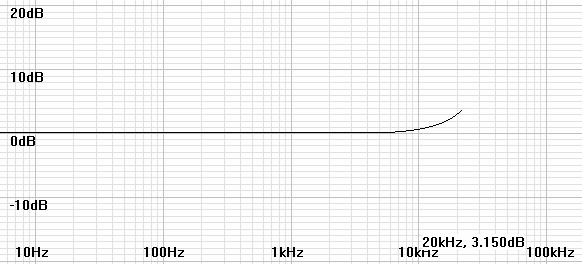Figure 6: Plot of H(z) for coefficients calculated for 96kHz with inverse RIAA.

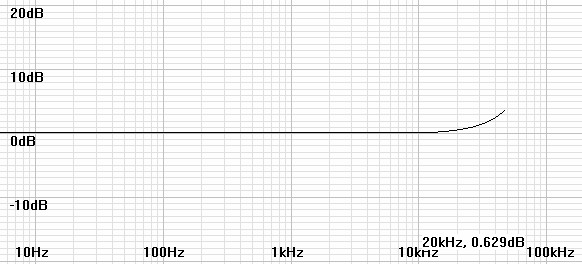Figure 7: Plot of H(z) for coefficients calculated for 192kHz with inverse RIAA.

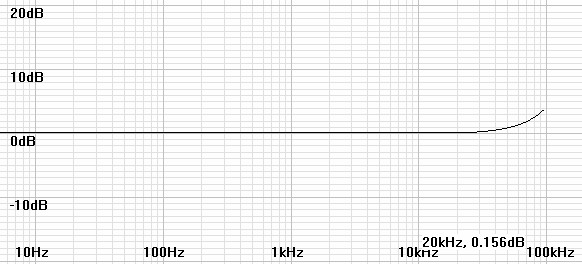As a practical matter the RIAA specification creates an impossible inverse RIAA filter - one with more zeros than poles - which is unrealizable in a real analog filter. A realizable analog inverse RIAA filter would have to add an extra pole at some arbitrarily high frequency. Reliable sources say that the predominant extra pole was at 50kHz. Therefore it is reasonable to ask whether this pole would mitigate the rise in the response at the anomaly. The following plots investigate this possibility.

Figure 8: Plot of H(z) for coefficients calculated for 44.1kHz with practical inverse RIAA.

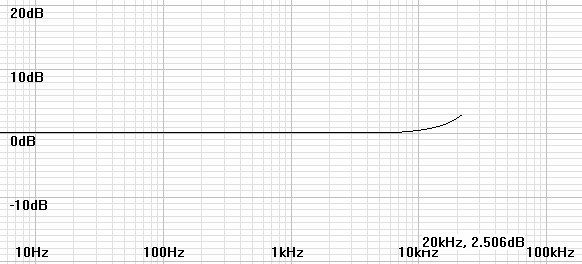Figure 9: Plot of H(z) for coefficients calculated for 96kHz with practical inverse RIAA.

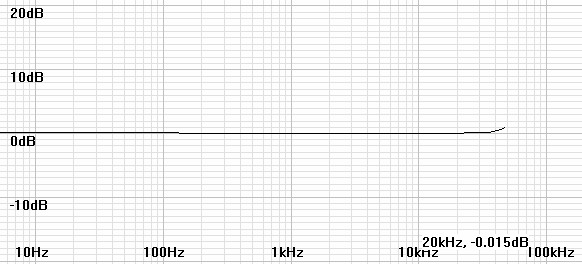Figure 10: Plot of H(z) for coefficients calculated for 192kHz with practical inverse RIAA.

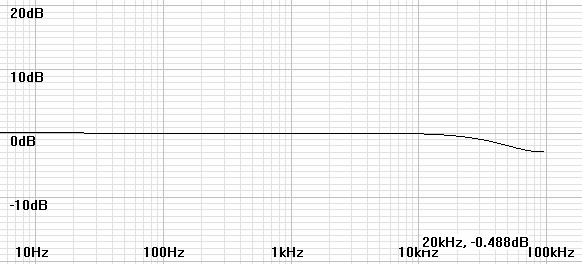The extra pole seems to benefit the 44.1kHz filter little, to compensate the 96kHz filter nearly perfectly, and to roll off the 192kHz filter only slightly.

Applying the filter to an audio file

At this point you might expect a program to equalize your files. However, I have found that a free audio editor - Audacity - has the facility to apply the calculated filters. I presume the program user-friendly to the degree that you can load your files and find your way around. Once the file is loaded execute the following procedure.

Connect turntable to an unequalized microphone input of a computer recording interface or stand-alone digital recorder.
Record the LP with as much gain as will not clip the recorder. If insufficient maximum gain causes excessive noise, a separate low-noise amplifier may be interposed between the turntable and recorder.
Open or import the recorded file into Audacity.
Setup Audacity to show where clipping occurs. Then red vertical lines will indicate clipping points.

Menu → View → Show Clipping

Upsample the file if its sampling rate is less than 88.2kHz. It is thought better to upsample by some power of 2: 2x, 4x, etc.

Menu → Tracks → Resample

Open the Nyquist prompt

Menu → Effects → Nyquist prompt...

Enter the nyquist biquad equation that the program generated. Note: If the dialog contains a check box labeled "Use legacy (version 3) syntax," check it. My current software only gives equations in LISP format not the newer SAL.

Example at 96kHz for a gain of one:
(biquad-m s 1.315951e-02 -1.273543e-02 0.000000e+00 1.000000e+00 -1.867054e+00 8.674785e-01)

If the gain changes to appear to clip, undo that step and find a way to proceed without clipping. At the actual filter step, recalculate the filter with an appropriate new gain and re-execute.
Make other alterations as desired: click removal, warp or rumble filtering.
Resample to original rate if desired.
Save project or export file. Exports 16-bit audio by default. Exporting 24 or 32 bit audio requires extra steps:

Menu → File → Export Audio...
Save as type: Other uncompressed files.
Click Options... and select header and encoding appropriate for the desired 24 or 32 bit export.
Click Save.

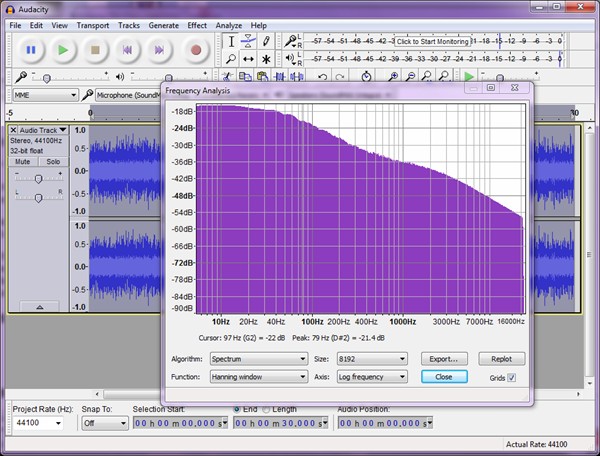
Figure 11: FFT shows that upsampling to 176.4kHz before equalization to return
to 44.1kHz leaves no apparent anomaly.

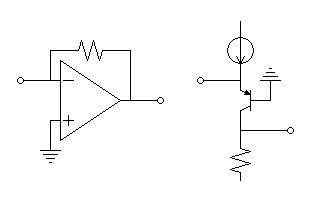
Current Input Preamplifier Additions

It seems that the extra zero available to the digital biquad filter could be used to implement equalization for a current-input preamplifier instead of the 50kHz extra zero that seems not to be needed for the voltage-input preamplifier already calculated. Figure 12 shows both op-amp and transistor current-input preamplifiers in the simplest form without added detail. In such a configuration, the input loop between the cartridge and preamplifier is a simple first-order lowpass filter determined by the inductance and resistance of the cartridge in use.

(12)

f_LR =

2πL

Caveat: Since figure 12 represents additional amplification, it might not be practical to drive a microphone preamplifier of already correct gain for a MM cartridge. Instead it could be used as a MC pre-preamp or drive a line-level ADC input instead.

Figure 12: Representative linear transimpedance amplifiers suitable for current input preamps.

The program has been altered so that entering an actual zero frequency instead of logical zero or one will calculate the biquad for the indicated current-input equalization. To begin you will have to obtain L and R values for your cartridge by measurement or documentation. These values can be obtained for some cartridges from the PhonoLCR program elsewhere on this site. Then calculate the LR frequency and enter it with the other parameters. The program will calculate a voltage-input equalization as before if logic zero or one values are entered for the zero.

Figure 13: riaaiir.c program listing adding option of current input zero.

      #include <stdio.h>

#include <string.h>

#include <math.h>

typedef struct {int nn, nd; double n[3], d[3];} biquad;

#define TP1 3180e-6

#define TP2 75e-6

#define TZ1 318e-6

#define TZ2 3.18e-6

#define PZ(T) exp(-1.0/(fs*(T)))

biquad computeriaaiir(double fs, double dcgain, double extrazero)

{

  static biquad bq;

  double p1, p2, z1, z2, gain;

  int i;

  p1 = PZ(TP1);

  p2 = PZ(TP2);

  z1 = PZ(TZ1);

  if(extrazero > 1.0)

    z2 = PZ(1.0/(2*acos(-1.0)*extrazero));

  else

    z2 = PZ(TZ2);

  bq.nd = 3;

  bq.d[0] = 1.0;

  bq.d[1] = -p1-p2;

  bq.d[2] = p1*p2;

  if(extrazero)

  {

    bq.nn = 3;

    bq.n[0] = 1.0;

    bq.n[1] = -z1-z2;

    bq.n[2] = z1*z2;

  }

  else

  {

    bq.nn = 2;

    bq.n[0] = 1.0;

    bq.n[1] = -z1;

    bq.n[2] = 0.0;

  }

  gain = (bq.n[0]+bq.n[1]+bq.n[2])/(1.0+bq.d[1]+bq.d[2]);

  for(i=0; i<3; i++)

    bq.n[i] *= (dcgain/gain);

  return bq;

}

void printbiquadcoeff(biquad bq)

{

  int i;

  for(i=0; i<bq.nn; i++)

    printf("\t%e",bq.n[i]);

  printf("\n------------------------------------------------\n");

  for(i=0; i<bq.nd; i++)

    printf("\t%e",bq.d[i]);

  printf("\n");

  printf("Audacity biquad equations\n");

  // believe a's are denominators

  printf("(biquad s b0 b1 b2 a0 a1 a2)\n");

  printf("(biquad s");

  for(i=0; i<3; i++)

    printf(" %e",bq.n[i]);

  printf(" 1.0");

  for(i=1; i<3; i++)

    printf(" %e",-bq.d[i]);

  printf(")\n");

  printf("(biquad-m s b0 b1 b2 a0 a1 a2)\n");

  printf("(biquad-m s");

  for(i=0; i<3; i++)

    printf(" %e",bq.n[i]);

  for(i=0; i<3; i++)

    printf(" %e",bq.d[i]);

  printf(")\n\n");

}

int main()

{

  biquad riaa;

  double fs, gain;

  double extrazero;

  do

  {

    printf("\nExtra zero options:\n0: No extra zero\n1:
Extra zero at 50kHz" \

    "\n>1: Frequency of extra zero to compensate for
lowpass rolloff of current input preamp");  

    printf("\n\nEnter sampling frequency, dc gain, and
0/1/f(current input LR freq) for extra zero:  ");

  }

  while(3 <
scanf("%lf%lf%lf",&fs,&gain,&extrazero));

  printf("\n");

  riaa = computeriaaiir(fs,gain,extrazero);

  printbiquadcoeff(riaa);

  printf("\n");

  return 0;

}

Click here to download Windows version 1.1.0 of the program with option of current-input zero. This Windows version requires a check mark be placed for any extra zero, then if the zero frequency entry is blank the default is 50kHz, otherwise the input value is taken.

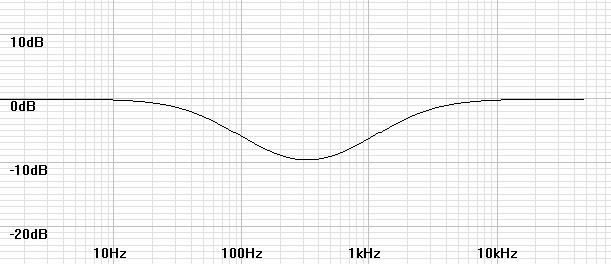
Figures 14 and 15 simulate the equalization and final responses of a typical current-input setup (perhaps some Pickering cartridges). Notice that the final response nearly has nearly no anomaly because the phase shift approaching ½f_s is nearly zero.

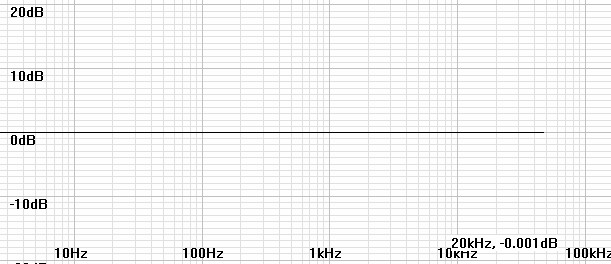
Figure 14: Plot of H(z) for coefficients calculated for f_s = 96kHz and f_LR = 212.2Hz.

Figure 15: Plot of H(z) for coefficients calculated for f_s = 96kHz and f_LR = 212.2Hz with inverse RIAA.

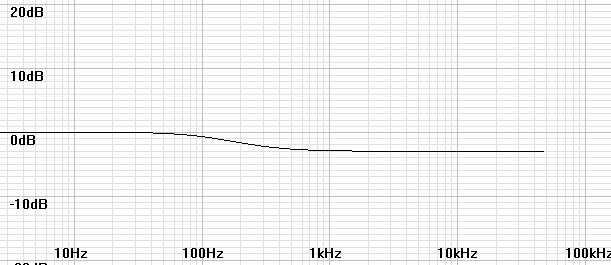
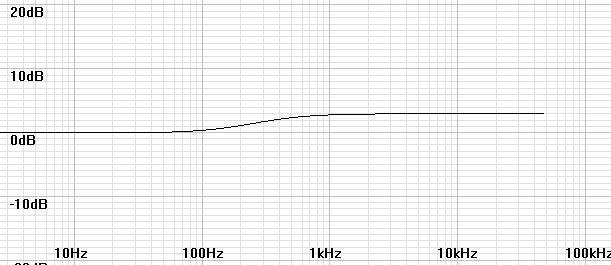
It may be that the L and R values used for your cartridge are inaccurate so that trial and error adjustments may be made to f_LR. The mismatch between a pole and a zero in the equalization creates a shelf filter like a bass or treble control and likewise can be adjusted by a sharp ear as the following graphs indicate.

Figure 16: Equalized with f_LR = 212.2Hz but actually f_LR = 150Hz. Adjust f_LR down.

Figure 17: Equalized with f_LR = 212.2Hz but actually f_LR = 300Hz. Adjust f_LR up.

Result of an actual test recording

Figure 18: Tascam DR-05 Digital recorder setup to record directly from turntable.

The idea for this article was actually based on recording directly to a high-resolution field recorder that I already possessed: a Tascam DR-05 purchased from Amazon.com for $89.

Before recording, I calculated the frequency response in PhonoLCR using the recorder's specified 25kΩ input impedance without changing the estimated capacitance to get near Butterworth response in order to estimate what changes in sound I might expect from the different cartridge loading. I connected my turntable directly to the MIC/EXT IN input and recorded according to the recorder's instructions at 24bit/96kHz. The recording level set to a level somewhere in the middle of the range, suggesting a good fit to the output of the MM cartridge that I was using. Monitoring on the headphones, pops and crackles were very loud but I expected later equalization to greatly lower it.

When finished, I equalized the recording in Audacity as I have detailed above. The first gain setting looked clipped so I recalculated the filter coefficients and tried again for correct results and returned the file to the recorder.

I only intended to verify that the equalization sounded correct, which it did. The recorder's noise floor also seemed well below that of the album as well. Many years ago I had recorded the same album with a CD recorder. Those results, though they seemed accurate, seemed flat compared to listening to the vinyl while the recording proceeded. The vibrant colors of the vinyl seem muted somehow. In contrast, this high resolution recording has the vivid colors like the album, perhaps better because the treble sounded more neutral, something I attributed to cartridge loading.

A test of current-input equalization await another time.

Inverse RIAA equalization additions

The new version of the program has added an inverse RIAA digital filter function. It seemed an easy addition that may be useful to someone. Perhaps it could create a test file to test the equalization of a phono preamp or to create preequalized masters for creating vinyl if record cutters allow any bypass of their inverse equalization filters.

Figure 19 below gives the listing of the expanded console program. All functionality is the same as before except for an additional variable entry to choose the inverse function. Then if the inverse function is chosen, the program swaps the numerator and denominator coefficients before they are adjusted for the specfied gain.

Figure 19: Version 1.2.0 riaaiir.c program listing adds an inverse RIAA digital filter function.

      #include <stdio.h>

#include <string.h>

#include <math.h>

typedef struct {int nn, nd; double n[3], d[3];} biquad;

#define TP1 3180e-6

#define TP2 75e-6

#define TZ1 318e-6

#define TZ2 3.18e-6

#define PZ(T) exp(-1.0/(fs*(T)))

biquad computeriaaiir(double fs, double dcgain, double extrazero, int
inverse)

{

  static biquad bq;

  double p1, p2, z1, z2, gain, tmp;

  int i, itmp;

  p1 = PZ(TP1);

  p2 = PZ(TP2);

  z1 = PZ(TZ1);

  if(extrazero > 1.0)

    z2 = PZ(1.0/(2*acos(-1.0)*extrazero));

  else

    z2 = PZ(TZ2);

  bq.nd = 3;

  bq.d[0] = 1.0;

  bq.d[1] = -p1-p2;

  bq.d[2] = p1*p2;

  if((int)extrazero)

  {

    bq.nn = 3;

    bq.n[0] = 1.0;

    bq.n[1] = -z1-z2;

    bq.n[2] = z1*z2;

  }

  else

  {

    bq.nn = 2;

    bq.n[0] = 1.0;

    bq.n[1] = -z1;

    bq.n[2] = 0.0;

  }

if(inverse)

  { /* swap numerator and
denominator */

    for(i=0; i<3; i++)

    {

      tmp = bq.d[i];

      bq.d[i] =
bq.n[i];

      bq.n[i] = tmp;

    }

    itmp = bq.nd;

    bq.nd = bq.nn;

    bq.nn = itmp;

  }

  gain = (bq.n[0]+bq.n[1]+bq.n[2])/(1.0+bq.d[1]+bq.d[2]);

  for(i=0; i<3; i++)

    bq.n[i] *= (dcgain/gain);

  return bq;

}

void printbiquadcoeff(biquad bq)

{

  int i;

  for(i=0; i<bq.nn; i++)

    printf("\t%e",bq.n[i]);

  printf("\n------------------------------------------------\n");

  for(i=0; i<bq.nd; i++)

    printf("\t%e",bq.d[i]);

  printf("\n");

  printf("Audacity biquad equations\n");

  // believe a's are denominators

  printf("(biquad s b0 b1 b2 a0 a1 a2)\n");

  printf("(biquad s");

  for(i=0; i<3; i++)

    printf(" %e",bq.n[i]);

  printf(" 1.0");

  for(i=1; i<3; i++)

    printf(" %e",-bq.d[i]);

  printf(")\n");

  printf("(biquad-m s b0 b1 b2 a0 a1 a2)\n");

  printf("(biquad-m s");

  for(i=0; i<3; i++)

    printf(" %e",bq.n[i]);

  for(i=0; i<3; i++)

    printf(" %e",bq.d[i]);

  printf(")\n\n");

}

int main()

{

  biquad riaa;

  double fs, gain;

  double extrazero;

    int inverse;

  do

  {

    printf("\nExtra zero options:\n0: No extra zero\n1:
Extra zero at 50kHz" \

    "\n>1: Frequency of extra zero to compensate for
lowpass rolloff of current input preamp" \

        "\nInverse options:  (0)
RIAA eq, (1) Inverse RIAA eq");

    printf("\n\nEnter sampling frequency,\ndc
gain,\n(0/1/f(current input LR freq)) for extra zero" \

        "\n(0/1) to select inverse:\n\n:
");

  }

  while(4 <
scanf("%lf%lf%lf%d",&fs,&gain,&extrazero,&inverse));

  printf("\n");

  riaa = computeriaaiir(fs,gain,extrazero,inverse);

  printbiquadcoeff(riaa);

  printf("\n");

  return 0;

}

Click here to download Windows version 1.2.0 of the program with inverse RIAA option. This Windows version requires a check mark be placed to invoke the inverse function. As before, it also requires check mark be placed for any extra zero, then if the zero frequency entry is blank the default is 50kHz, otherwise the input value is taken. Also note that any extra zero specified becomes a pole in the inverse filter.

Figure 20: Entry dialog for version 1.2.0 of the Windows program

I verified the results by plotting frequency response for many combinations of combined RIAA and like specified inverse RIAA filters to get perfectly flat responses in all cases. Having proven that the inverse filters are exact inverses their response can be inferred by examining the responses of the corresponding non-inverted plots above.. Figure 21 below shows a representative inverse RIAA response.

Figure 21: Plot of H(z) for coefficients calculated for 192kHz inverse filter with extra pole.

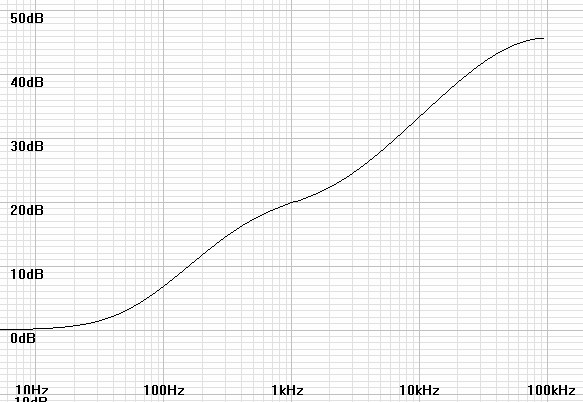Final remarks

You might argue that Audacity has a FIR RIAA filter built in, however blogs inquiring whether they had correct or linear phase resulted in someone saying that phase correction did not matter. This uncertainty leaves me another reason to stay with an IIR design.

This is a large topic. Therefore there may be later additions.

Document History
June 6, 2015 Created.
June 11. 2015 Corrected a misspelling and added an extra step to each of the compilation of riaaiir and the Audacity filtering process.
September 1, 2015 Added capability to digitally equalize a current-input preamplifier.
September 7, 2015 Added Results of an actual test recording.
May 3, 2016 Added inverse RIAA functionality to software.