Home  │ Audio Home Page

Copyright © 2011 by Wayne Stegall
Updated November 4, 2011.  See Document History at end for details.

Phono Preamp Input Protection

Dilemma

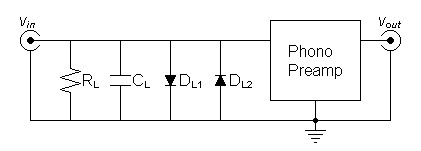
On first impulse it seems advisable to protect the front end of a phono preamp with a circuit such as in figure 1.  The clamping diodes are able to protect from the real possibility that a line output could be connected to a phono input.  However, reservations about the distortion produced by the diodes may deter their actual use.  I expect you too have similar concerns.  In view of their usefulness however, it would be better to analyze the circuit before making a hasty decision.

Figure 1:  Diodes protecting phono preamp input

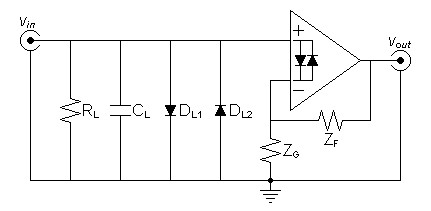
A Typical Example

A typical illustration of the need of input protection for a phono preamp is illustrated in figure 2.  Here a typical low-noise bipolar operational amplifier has internal protection diodes limited to 10mA to protect.  Without protection, Z_G may allow excessive current to flow through internal diodes damaging an expensive operational amplifier.  Discrete circuits could present similar difficulties, i.e. an overloaded JFET could see reverse gate current exceeding specifications in spite of some protection by a source resistor.

Figure 2:  Example of diodes protecting bipolar operational amplifier

ZF and ZG here simplify a more complicated RIAA equalization circuit. Internal protection diodes are taken out of the signal path by the feedback loop in normal operation.

Here the voltage across Z_G causes the external diodes to shunt the majority of current that would pass through the internal diodes if the input is overloaded.  Because diodes have an exponential transconductance characteristic, addition of voltages multiplies currents and subtraction of voltage divides currents by commonly known exponential and logarithmic relations.

Exponential Axioms		Corresponding Logarithmic Axioms
(1) ex+y  = ex × ey (2) ex-y  = ex ey		(3) ln(a) + ln(b)  = ln ( a × b ) (4) ln(a) - ln(b)  = ln a b

Where V_e is the limiting voltage across the external diodes, V_i that across the internal ones, and V_zg that across Z_G, the following voltage subtraction creates a related current bypass ratio:

(5)	Vi = Ve - Vzg

Solve for the current bypass ratio presuming external protection diodes have the same saturation current I_O as the internal ones:

(6)

Iext Iint

=

IO(e40×Ve - 1) IO(e40×Vi - 1)

=

e40×Ve - 1 e40×Vi - 1

Under the overload conditions of interest, e^40×V >> 1, therefore:

(7)

Iext Iint

=

e40×Ve e40×Vi

=

e40×(Ve-Vi)

=

e40×Vzg

In the limiting condition where a Z_G of 10Ω passes 10mA and drops 100mV:

(8)

Iext Iint

=

e40×(100mV)

=

e4

=

54.5982

This means the external protection diodes will bypass 545.982mA before the op-amp input diodes exceed their specifications, conditions easily met by reasonable overload conditions.  This is well below the current output limit of most operational amplifiers and the output of circuits with limiting resistors as well.  Only the improbable connection of speaker leads to the protected input could damage the operational amplifier.  The sacrifice and replacement of a 1N914 or a 1N4148 small signal diode is well worth protecting more expensive circuitry, although a medium diode like a 1N4004 might absorb all current from any line output without destruction.

More Exact Calculations

My presumption in the above calculations that the saturation currents are equal served the purpose of demonstration, because I knew it to be a worst case example.  Actual saturation current, however, is roughly proportional to the size and current capacity of the diode.  I expected the operational amplifiers input protection diodes to be smaller than any external ones used for protection and to result in a greater current bypass ratio.

If the presumption of equal I_O were not met equation 7 would have been:

(9)

Iext Iint

=

IO-ext IO-int

× e40×Vzg

Consider some actual saturation currents:

Diode		IO
AD797 input protection		1.0fA
1N914		64.7335pA
1N4001		31.9824nA

Still in the limiting condition where a Z_G of 10Ω passes 10mA and drops 100mV,
now an AD797 protected by 1N914's gives:

(10)

Iext Iint

=

64.7335pA 1.0fA

× e40×(100mV)

=

64.7335k × e4

=

3.53433M(A/A)

In this case the 1N914 would have to pass an impossible 35kA before the internal diodes reached their limit of 10mA.

and an AD797 protected by 1N4001's gives:

(11)

Iext Iint

=

31.9824nA 1.0fA

× e40×(100mV)

=

31.9824M × e4

=

1.74618G(A/A)

In this case the 1N4001 would have to pass an absurd 17MA before the internal diodes reached their limit of 10mA.

Either of these real results leave the operational amplifer to bear negligible overload current.

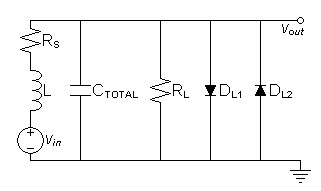
SPICE Analysis

The following is the distortion analysis of a typical MM phono input loop.

Figure 2:  SPICE schematic.

SPICE model

Fourier analysis of v_out for v_in of 5mV_RMS protected by 1N914s:
  No. Harmonics: 16, THD: 6.20501e-06 %, Gridsize: 200, Interpolation Degree: 1

Harmonic	Frequency	Magnitude		Norm.Mag		Percent		Decibels
1	1000	0.00696354		1		100		0
3	3000	3.5818e-10		5.14364e-08		5.14364e-06		-145.775
5	5000	6.19818e-11		8.9009e-09		8.9009e-07		-161.011
7	7000	7.47346e-11		1.07323e-08		1.07323e-06		-159.386
9	9000	8.88345e-11		1.27571e-08		1.27571e-06		-157.885
11	11000	1.03415e-10		1.48509e-08		1.48509e-06		-156.565
13	13000	1.17256e-10		1.68386e-08		1.68386e-06		-155.474
15	15000	1.29017e-10		1.85275e-08		1.85275e-06		-154.644

Even harmonics were omitted because the minuscule values calculated represent only calculation noise inconsistent with circuit symmetry expecting their values to be zero.

Distortion here is vanishingly low!

I initially preferred the use of small signal diodes to medium ones because I expected the distortion to increase with the saturation current.  So here I add a distortion analysis with a medium diode as well.

Fourier analysis of v_out for v_in of 5mV_RMS protected by 1N4001s:
  No. Harmonics: 16, THD: 0.000811766 %, Gridsize: 200, Interpolation Degree: 1

Harmonic	Frequency	Magnitude		Norm.Mag		Percent		Decibels
1	1000	0.00696751		1		100		0
3	3000	5.65599e-08		8.11766e-06		0.000811766		-101.811
5	5000	2.24354e-11		3.22001e-09		3.22001e-07		-169.843
7	7000	1.34994e-14		1.93748e-12		1.93748e-10		-234.255
9	9000	2.00863e-14		2.88285e-12		2.88285e-10		-230.804
11	11000	4.37608e-14		6.2807e-12		6.2807e-10		-224.040
13	13000	4.30256e-14		6.17517e-12		6.17517e-10		-224.187
15	15000	1.82514e-14		2.6195e-12		2.6195e-10		-231.636

Even harmonics were omitted because the minuscule values calculated represent only calculation noise inconsistent with circuit symmetry expecting their values to be zero.

The third harmonic here has increased as expected until it is low but no longer vanishing.  It is odd that the remaining harmonics have decreased.

Last Word

Because diode distortion is presumed more objectionable than that of FETs and tubes, It is still a subjective matter whether an input protector's distortion is acceptable in your circuit.

Document History
November 3, 2011  Created.
November 3, 2011  Made improvements.  Added much new material.  Updated SPICE results based on better diode models.
November 4, 2011  Corrected some grammar.