Home │ Audio Home Page

Copyright © 2011 by Wayne Stegall
Updated June 14, 2011. See Document History at end for details.
Partially SPICE Verified

Distortion Cancelation

Three simple distortion cancelation concepts.

Introduction

It is the purpose of this article to introduce simple distortion cancelation concepts. All function to linearize one device with another device having the same transfer equation perhaps scaled in some applications. The transfer functions are represented in this article as follows:

Transconductance transfer function

(1)

i = g(v)

Transimpedance transfer function

(2)	v = g^-1(i)

In this designation the suffix ^-1 indicates an exact inverse equation so that:

(3)	g^-1(g(x)) = g(g^-1(x)) = x

This relation relates the mathematical operation of the first two distortion cancelation techniques.

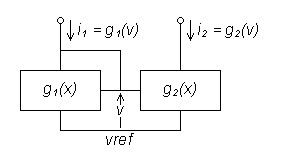
Current Mirror

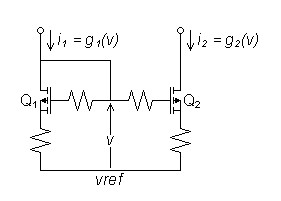
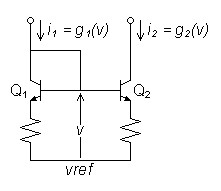
Figure 1: Generalized Current Mirror	Figure 2: MOSFET Current Mirror	Figure 3: BJT Current Mirror

Figure 4: Graph Illustrating Current Mirror Operation

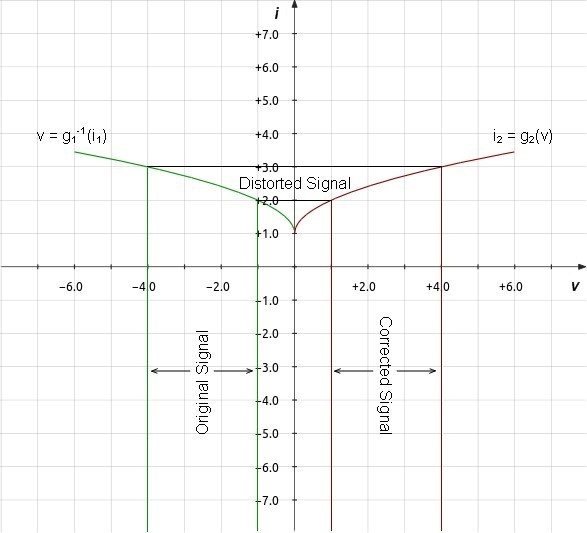A current mirror duplicates its input current in the output by means which cancel distortion. The input transistor or amplification block converts current to voltage by the inverse of the transfer function g₁(x) by which the second amplification block converts voltage to current:

Transimpedance creates distortion.

(4)	v = g₁^-1(i₁)

Distortion cancelation removes it.

(5)	i₂ = g₂(v)

Because g₁(x) = g₂(x):

(6)	i₂ = g₂(g₁^-1(i₁)) = g₁(g₁^-1(i₁)) = i₁

Transistors and feedback resistors must be in matched pairs. Because the feedback resistors are present to reduce any semiconductor mismatches, they are often omitted when the matched transistors are created equally on the same silicon die. I.e. in an IC or a dual transistor device.

If you can pair devices so that the transfer curves match on a scale, current amplification is possible.
Assuming g₂(x) = A_CURR × g₁(x):

(6)	i₂ = g₂(g₁^-1(i₁)) = A_CURR × g₁(g₁^-1(i₁)) = A_CURR × i₁

This attempt to add gain may shift the voltage bias so that the transconductance blocks may require termination by different reference voltages to restore proper distortion cancelation, however.

Equations adding gain to the current mirror above and the voltage mirror below extrapolate from presumptions based on linear devices. Actual results may vary and calculations based on device parameters will depend on the extent to which the non-linear transfer curve has scale symmetry and will differ according to the device used.

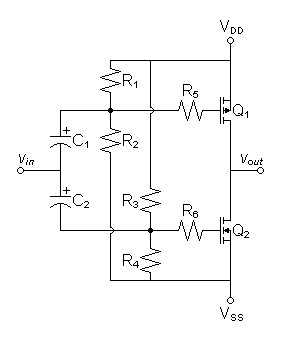
Voltage Mirror

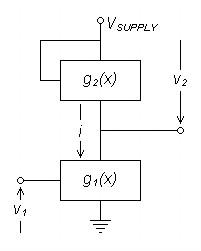
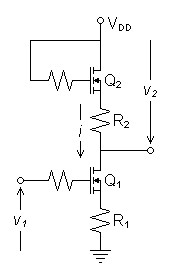
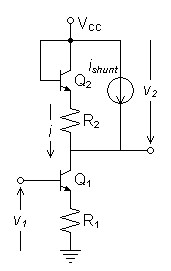
Figure 5: Generalized Voltage Mirror	Figure 6: MOSFET Voltage Mirror	Figure 7: BJT Voltage Mirror	Figure 8: Integer Gain BJT Voltage Mirror

Figure 9: Graph Illustrating Voltage Mirror Operation

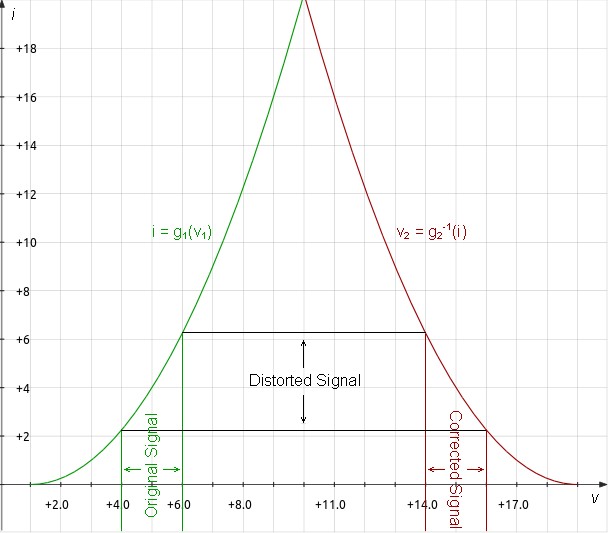The voltage mirror duplicates the input voltage at the output by means which cancel distortion. The amplifying block converts voltage to current by the same transfer function g₁(x) as the distortion cancelation device uses to cancel distortion, designated g₂(x) to allow scaling.

Transconductance creates distortion.

(7)	i = g₁(v₁)

Distortion cancelation removes it.

(8)	v₂ = g₂^-1(i)

Because g₁(x) = g₂(x):

(9)	v₂ = g₂^-1(g₁(v₁)) = g₁^-1(g₁(v₁)) = v₁

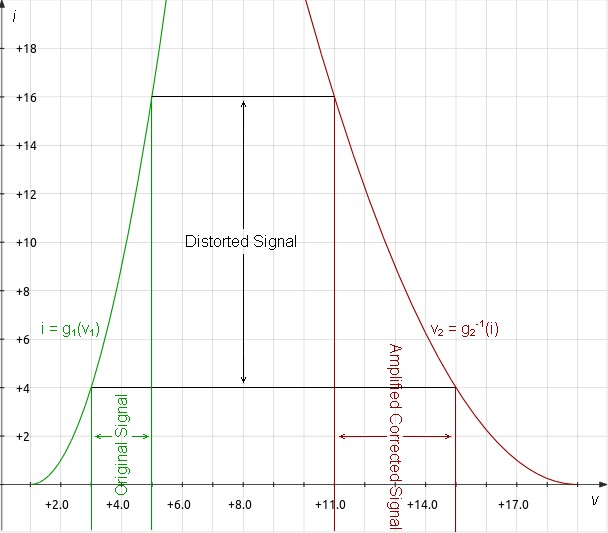
Because distortion here is cancelled in a common-source or common-emitter circuit where gain is expected, the cancelation factors must be scaled. Assuming g₁(x) = A_V × g₂(x), therefore g₂^-1(x) = g₁^-1(A_V × x) and:²

(10)	v₂ = g₂^-1(g₁(v₁)) = g₁^-1(A_V × g₁(v₁)) = A_V × v₁

Figure 10: Graph Illustrating Amplified Voltage Mirror Operation

FET specifics

Because the resistors must be scaled inversely to the transconductance parameters, the following relations hold:¹

(11)	g_fs1 = A_V × g_fs2
(12)	R₂ = A_V × R₁
(13)	g_fs1 × R₁ = g_fs2 × R₂

Because the mirror is connected by the common drain current and

(14)

g_fs = 2 x

k_nI_D

Relations involving k_n can be established

(15)	k_n1 = A_V² × k_n2
(16)	k_n1 × R₁² = k_n2 × R₂²

BJT specifics

The exponential transfer function of the BJT permits distortion cancelation. This is because the exponential function involved has a unique symmetry where scaling the current appears to shift the same curve to a different voltage bias.

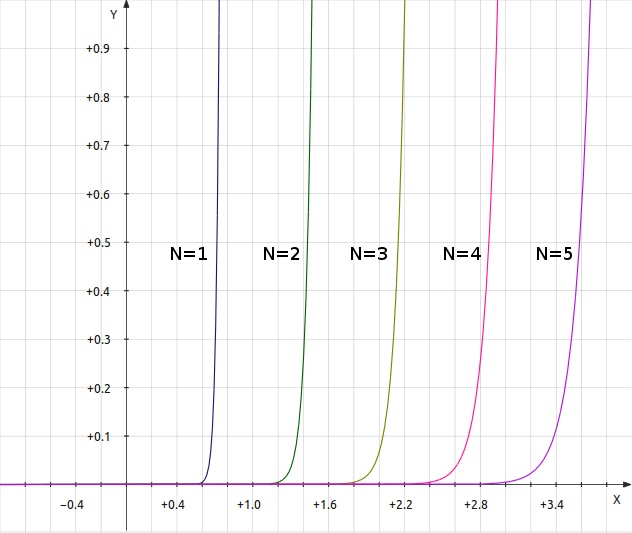
The base-to-emitter PN junction (diode) that creates this unique symmetry has the function and is illustrated in figure 11 below for N=1:

(17)	i_pn = i₀(e^v/VT-1)

Because the resistors must be scaled inversely to the transconductance parameters, the following relations hold for gain A_V:

(18)	g_m1 = A_V × g_m2
(19)	R₂ = A_V × R₁
(20)	g_m1 × R₁ = g_m2 × R₂

Where the characteristic PN voltage V_T ≈ 25mV, transconductance is proportional to current:

(21)

g_m =

I_E

V_T

≈

I_E

25mV

This works well enough if the gain is one.

Topology Compensating in Gain with One Compensation Device (Not recommended).

Thus to lower g_m2 relative to g_m1 to set cancelation with gain in one device, it is necessary to lower the current bias through Q₂. Figure 7 shows the use of a DC current shunt around the cancelation circuit to accomplish this objective. That the DC bias voltage across R₁ and R₂ are equal as a result of this adjustment if the transistors are matched is a convenient coincidence.

Because g_m is tied to bias current for any PN junction according to equation (21), no one device can compensate for a BJT in a gain situation without current bias change.

I believe now that this method destroys symmetry and the resulting distortion reduction is done at the sacrifice of creating two bends in the transfer curve. Without symmetry, it is not strictly a voltage mirror. Use the following topology instead. I intend to delete this topology from the article once I am sure of this outcome.

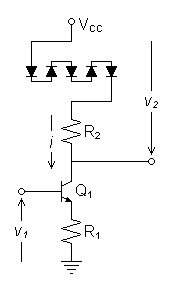
Integer Gain BJT Voltage Mirror Topology (Preferred Topology)

For integer gain of N, a direct solution is to use N compensation devices in the load as in figure 8. The combined transconductance for N series compensation devices is:

(22)

g_m2 =

I_C

N × V_T

≈

I_C

N × 25mV

If g_m1 is calculated by equation (21) and g_m2 by equation (22) and , equations (18)-(20) relate the design equations for gain. This would have been the first topology to try had it not been for my bias against using so many diodes or transistors in the compensation circuit. However, this bias may not have any validity as the shared current forces all of the diodes to respond as one. There are practical limits to N however; consider that ten diodes will drop about 7V.

Figure 11: I/V Curve of Series Diodes Scale with Symmetry with Increase in N.

Square Law cancelation

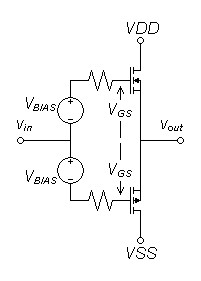
Figure 12: MOSFET Push-pull Common Source Amplifier	Figure 13: MOSFET Push-pull Voltage Follower

Figure 14: Graph Illustrating Square Law Distortion Cancelation

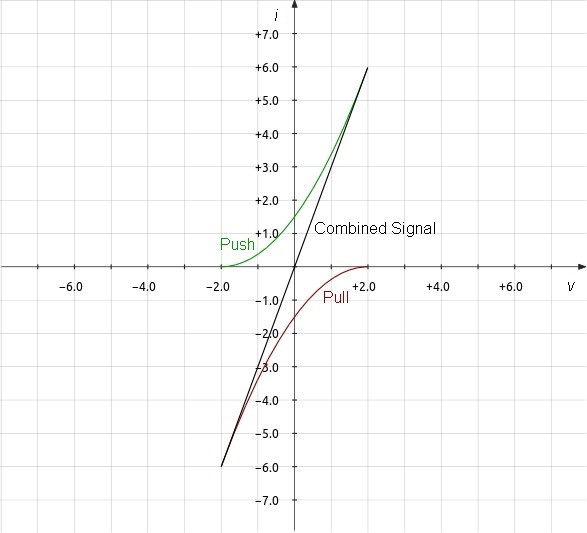square law distortion cancelation diagram

That FETs and vacuum tubes have square-law transfer curves enable a common distortion cancelation technique. Arrange two square law devices so that their linear signal components add while their second-order components subtract.

In the case of opposing n-ch and p-ch FETs:¹

(23)	I_Dn = k_n(V_GSn - V_Tn)²
(24)	I_Dp = k_p(V_GSp + V_Tp)²

If they are connected to oppose one another:

(25)	I_OUT = k_n(V_GS - V_Tn)² - k_p(V_GS + V_Tp)²
(26)	I_OUT = k_n(V_GS² - 2V_GSV_Tn + V_Tn²) - k_p(V_GS² + 2V_GSV_Tp + V_Tp²)
(27)	I_OUT = (k_n(-2V_GSV_Tn) - k_p(2V_GSV_Tp)) + (k_n(V_GS² + V_Tn²) - k_p(V_GS² + V_Tp²))
(28)	I_OUT = (k_n + k_p)(-2V_GS)(V_Tn + V_Tp) + (k_n - k_p)V_GS² + (k_nV_Tn² - k_pV_Tp²)

If k_n = k_p then second order term cancels leaving:

(29)	I_OUT = (k_n + k_p)(-2V_GS)(V_Tn + V_Tp)

The term (k_nV_Tn² - k_pV_Tp²) is constant and infers biasing which was omitted for simplicity.

If cancelation is imperfect the result will be as if the circuit were single-ended, the transfer curve bent in the direction of the greater of k_n or k_p. Adding source resistors in this application will increase distortion by altering the square-law transfer characteristic. They should only be added to correct imbalances between device source or cathode ohmic resistances if necessary.

Any difficulty in matching devices could be overcome by using dual FET arrays of the same polarity packaged in a single semiconductor. This would require transformer coupling on both the input and output to correctly juxtapose the device characteristics to produce this result, a typically tube topology.

SPICE Results

Current Mirror

Current mirrors are well established enough in principle for unity gain versions not to need SPICE verification yet.

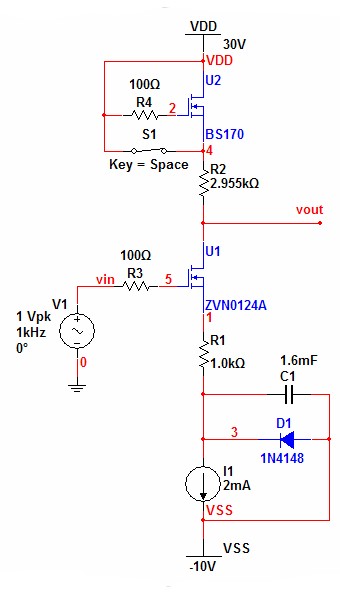
Voltage Mirror

Figure 15: SPICE Example: Amplified MOSFET Voltage Mirror

A preliminary SPICE evaluation of a unity gain MOSFET voltage mirror gave near perfect results. Calculate distortion correction for SPICE simulation of amplified MOSFET voltage mirror:

Given
k_n1 of ZVN0124A = 1.077A/V²
k_n2 of BS170 = 123.3mA/V²
and R₁ = 1kΩ

Calculate R₂ for distortion cancellation and arbitrary gain
from equation (16) above:

R₂ = R₁ ×

k_n1

k_n2

= 1kΩ ×

1.077A/V²

123.3mA/V²

= 2.95547kΩ

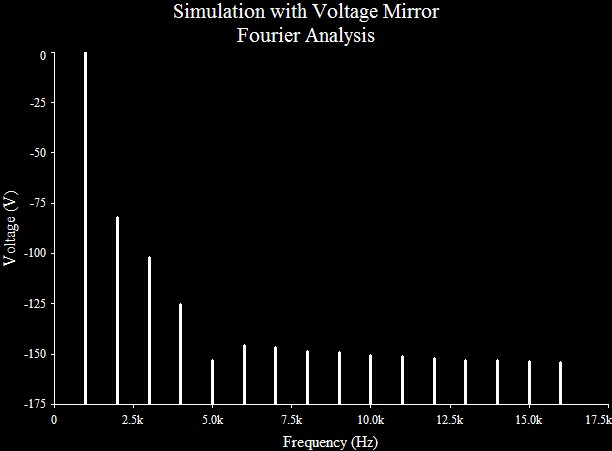
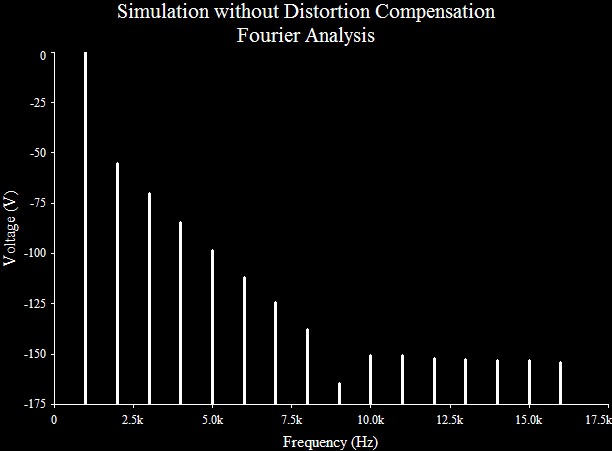
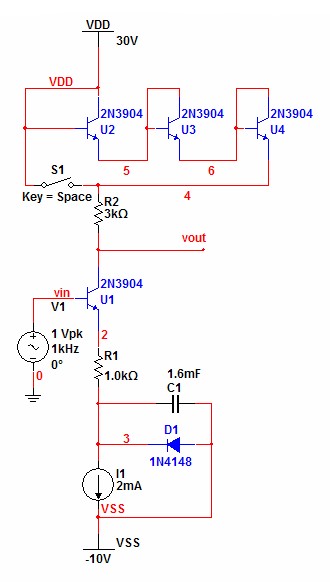
SPICE Model - Amplified Voltage Mirror (Multisim Analog Devices Version 10.0.1).

For the simulation, switch S₁ is provided to compare the results. If S₁ is open the circuit operates with distortion cancelation. As such the distortion result was 0.0000465395%. Closing S₁ bypasses the distortion cancelation. This result was 0.100808%. The graphs below show the details.

The preliminary simulation without gain produced similar results.

SPICE Model - Unity Gain Voltage Mirror (Multisim Analog Devices Version 10.0.1).

If you are curious, the subcircuit consisting of I₁, C₁, and D₁ represent an idealized autobias circuit. C₁ holds the voltage bias that would be required for AC fluctuation about a DC bias current of I₁. Calculate the highpass pole R₁C₁ for a low frequency minimizing any affect on bass response.

C₁ =

2πf_hpR₁

2π × 0.1Hz × 1kΩ

= 1.59155mF

Round up to 5% value:
C₁ = 1.6mF
(In practice, I should have chosen a 20% value of 2.2mF)

spice example - amplified voltage mirror

Figure 16: MOSFET Voltage Mirror Distortion Profile. Switch S1 open

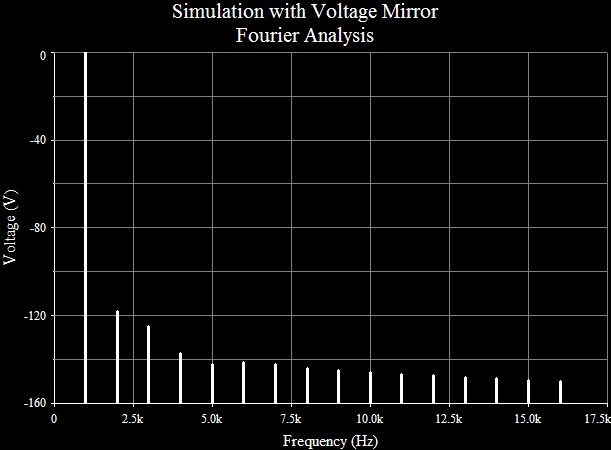Figure 17: MOSFET Distortion profile with Compensation Bypassed. Switch S1 closed.

Note: The similarity of the distortion plots above the 7th harmonic may indicate interpolation noise rather than any real differences at such low levels.

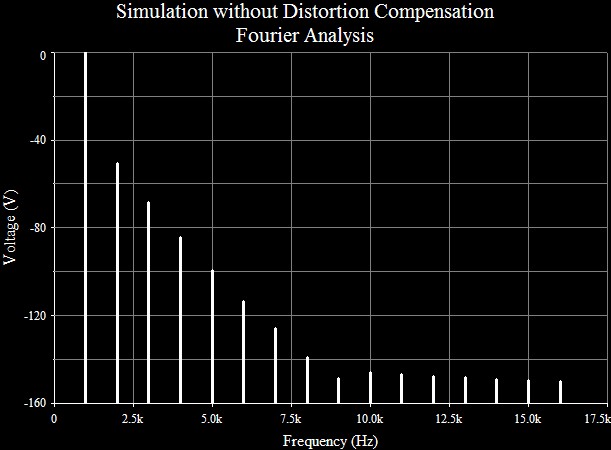BJT Voltage Mirror

Figure 18: SPICE Example: Integer Gain BJT Voltage Mirror

SPICE verified excellent results with the BJT voltage mirror only for unity gain. With gain, SPICE showed inconsistent results. I believe the culprit is the topology that reduces bias to the load. Decreasing bias by the same ratio by which the signal is increased is a bad idea. Distortion is inversely proportional to bias, the reduction in bias possibly eliminating any gains created by the compensation circuit. Experimentally however, some values of load current bias produced excellent cancelation results, but not those calculated. It is possible that distortion cancelation increases as the load bias current decreases toward the target until proximity to signal clipping ends any further gains.

Initial evaluation of an integer gain BJT voltage mirror produced ambiguous results until I thought the uncompensated circuit had such low distortion that interpolation error in SPICE might obscure any improvement. Only after I reduced the bias until the uncorrected circuit showed modest distortion was I able to demonstrate distortion cancelation. For the SPICE Example: Integer Gain BJT Voltage Mirror of figure 18 distortion cancelation lowered the distortion from 0.176063% to 0.0076505%.

Figure 19: BJT Voltage Mirror Distortion Profile. Switch S1 open

Figure 20: BJT Distortion profile with Compensation Bypassed. Switch S1 closed.

Push-pull Common Source Amplifier Model Demonstrating square-law cancelation

Figure 21: SPICE Example Push-pull Common Source Amplifier

This circuit is so simple that you may have seen it before.

SPICE Model - Push-pull Common Source Amplifier (Spice Opus version 2.31)

This model is setup for perfect distortion calculation with plausible MOSFET models. Only the third harmonic has any significance at -90dB. Distortion analysis is done at a peak voltage only half that of the supply because the non-feedback circuit exhibits soft-clipping at peak voltages approaching supply voltage.

Fourier analysis for vout:
No. Harmonics: 16, THD: 0.00308134 %, Gridsize: 1024, Interpolation Degree: 3

Harmonic	Frequency	Magnitude	Norm. Mag	Percent	Decibels

1	1000	11.0989	1	100	0
2	2000	1.89998e-08	1.71186e-09	1.71186e-07	-175.3306351
3	3000	0.000341991	0.000030813	0.0030813	-90.22532032
4	4000	6.13527e-10	5.5278e-11	5.5278e-09	-205.1489536
5	5000	1.71547e-06	1.54562e-07	1.54562e-05	-136.2179454
6	6000	2.87887e-10	2.59383e-11	2.59383e-09	-211.7211698
7	7000	1.82522e-07	1.6445e-08	1.6445e-06	-155.6793224
8	8000	2.36409e-10	2.13001e-11	2.13001e-09	-213.4323672
9	9000	2.05443e-08	1.85102e-09	1.85102e-07	-174.6517778
10	10000	1.93555e-10	1.74391e-11	1.74391e-09	-215.1695186
11	11000	2.38049e-09	2.14479e-10	2.14479e-08	-193.3723045
12	12000	1.63528e-10	1.47337e-11	1.47337e-09	-216.6337635
13	13000	3.27712e-10	2.95265e-11	2.95265e-09	-210.5957606
14	14000	1.36697e-10	1.23162e-11	1.23162e-09	-218.1904653
15	15000	1.27771e-10	1.1512e-11	1.1512e-09	-218.7769844

¹SPICE MOSFET models represent both k_n and k_p as KP. JFET models call this parameter BETA.
²I am taking some liberties with my math here because of the expectation of scale symmetry between g₁(x) and g₂(x).

Document History
May 26, 2011 Created.
May 26, 2011 Made minor improvements and corrections as noticed. Added scematic for SPICE example push-pull common-source amplifier and changed corresponding spice deck to match new component labels.
May 27, 2011 Corrected some hasty presumptions pertaining to adding gain to mirror circuits, particularly equations relating A_V to k_n for the MOSFET voltage mirror.
May 27, 2011 Added graphs illustrating distortion cancelation concepts.
May 31, 2011 Added SPICE verification of MOSFET voltage mirrors.
June 8, 2011 Recommended use of voltage mirror for BJT circuits only for unity gain pending further investigation. SPICE results problematic with gain, only unity gain producing the desired results. See text.
June 11, 2011 Added SPICE verification of integer-gain BJT voltage mirror.
June 14, 2011 Corrected a spelling mistake.