DAC Cascode

Analog DAC circuit designed with one BJT

Introduction

Current to voltage conversion is commonly needed to convert the output of many DACs. For any who requires a single transistor converter rather than the usual op-amp I/V converter, the BJT cascode is most obvious candidate.

PNP Circuit

Figure 1: Schematic of single-ended analog circuit..

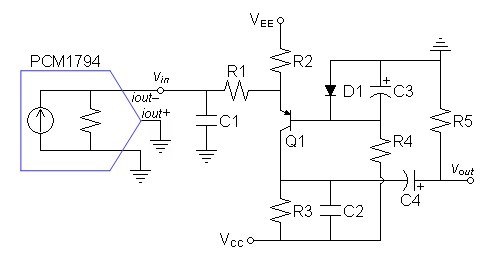Note: Only left channel shown. Duplicate for the right channel.

The circuit of figure 1 above adds several features to the ordinary BJT cascode of Q₁. R₂ increases the bias through Q₁ to lower overall distortion. D₁ biases the emitter of Q₁ to ≈ 0V. C₃ removes nonlinearities from drive to Q₁ base for the calculated range of higher frequencies and prevent RF from intermodulating in D₁. C₁ and C₂ create two synchronous lowpass poles with respect to their related resistances to give an overall cutoff frequency of 100kHz. C₁ in particular is positioned before Q₁ to reduce intermodulation with DAC RF frequencies. R₁ is added to reduce variations in AC emitter impedance related to signal level which tend to create a changing pole frequency with respect to C₁. As for the unused diffential DAC output, it is reasonable to connect it separately to the same voltage that the other sinks into.

This design for the PCM1794 will also work for the comparable PCM1792 also. For other current output DACs as the other PCM179x (the PCM1795, PCM1796, and PCM 1798), it would be necessary to recalculate for the different current output specifications. If the DAC sinks current rather than sources it as these do, the circuit polarity could be flipped and an NPN transistor used instead of a PNP. The AD1955 is one of these, not only requiring a NPN design but slightly different biasing as well.

First Try with PCM1794

I set R₃ and R₅ to the same value in the first attempt thinking R₃ could drive an equal resistance in R₅ with R₅ perhaps off the circuit board at the output jack. Placing R₅ at the end of dedicated interconnects could even eliminate cable effects.

Evaluate Datasheet

The datasheet for the PCM1794 gives the following output specifications:

AC output		7.8mA peak-to-peak for each single-ended output (I use the 3.9mA peak value in the calculations)
DC offset		–6.2mA
Output impedance		Unspecified

Because the DAC topology seems to source current rather than sink it the negative current value seemed unintuitive to me, I expected it to be positive. As a result, I examined the remainder of the datasheet for other clues. The ones I found were:

The recommended analog circuits show output driving virtual ground at operational amplifier.
DAC has only positive voltages to drive the 0V virtual ground.
Digital output current specifications are consistent with attributing positive current polarity with current sinking.

Other datasheets I have examined seem to attribute positive current polarity to current sourcing, so examine your datasheets and recommended circuits carefully for consistency.

As for polarity, if an op-amp i/v converter could be considered inverting, the BJT cascode is non-inverting by comparison with regard to the AC signal. Therefore the DACs polarity designations should be interpreted as reversed: the –i_out will actually be +i_out. As always examine the example analog circuit in the datasheet to verify this.

Design

Begin by calculating two synchronous pole frequencies which together will roll off at 100kHz:

(1)

α =

² 2

– 1

= 0.643594

(2)

f_stage =

f_system

100kHz

0.643594

= 155.377kHz

Choose V_EE = 15V
Choose V_CC = –30V to give room for desired bias.
Calculate R₃ and R₅ to convert 3.9mA input signal to 2V_RMS output signal

(3)

R₃ =

2 × 1.41421 × 2V

3.9mA

= 1.45048kΩ

Round down to nearest 1% value:
R₃ and R₅ = 1.43kΩ

Calculate R₂ for 5V headroom below ground:

(4)

I_Q1 =

30V – 5V

1.43kΩ

= 17.4825mA

(5)

I_R2 = 17.4825mA – 6.2mA – 1.95mA = 9.33252mA

(6)

R₂ =

15V

9.33252mA

= 1.60728kΩ

Round to nearest 5% value:
R₂ = 1.6kΩ

Calculate C₂ for second synchronous lowpass pole:

(7)

C₂ =

2πf_poleR_POLE

2π × 155.377kHz × (1.43kΩ/2)

= 1.43261nF

Round down to nearest 5% value:
C₂ = 1.3nF

To prepare to calculate for first lowpass pole, calculate an R₁ value to add with the AC emitter impedance to total about 10Ω.
First calculate minimum emitter current.

(8)

I_Q1-MIN =

1.6kΩ

+ 6.2mA – 3.9mA = 11.675mA

Then calculate maximum emitter impedance:

(9)

Z_Q1E-MIN =

25mV

11.675mA

= 2.14133Ω

Then calculate R₁.

(10)

R₁ = 10Ω – 2.14133Ω = 7.85867Ω

Decide to round up to nearest 5% value:
R₁ = 8.2Ω

Now C₁ can be calculated.

(11)

C₁ =

2πf_poleR_POLE

2π × 155.377kHz × (2.14133Ω + 8.2Ω)

= 99.0506nF

Round to nearest 5% value:
C₁ = 100nF

Calculate 1W R₄ to dissipate ½W:

(12)

R₄ =

V²

(30V – 0.7V)²

0.5

= 1.71698kΩ

Round to nearest 5% value:
R₄ = 1.8kΩ

Initially I arbitrarily chose C₃ = 47µF but decided to calculate for a subsonic pole, however the 750µF I calculated against the Q₁ base input impedance should have instead have been calculated against the ac impedance of D₁. In that case, a subsonic pole could not be achieved without an impractically enormous value for C₃. Until now leave as is.

Calculate C₄ for a time constant of 1s.

(13)

C₄ =

R_POLE

1.43kΩ + 1.43kΩ

= 349.6503497µF

Round to nearest 10% value:
C₄ = 330µF

Parts List
Q₁	2N3906 PNP	R₅	1.43kΩ 1% ½W or 1W
D₁	1N914 or 1N4148	C₁	100nF 5% plastic
R₁	8.2Ω 5% ¼W	C₂	1.3nF 5% plastic
R₂	1.6kΩ % ½W	C₃	47µF 10% aluminum electrolytic
R₃	1.43kΩ 1% 1W	C₄	330µF 10% aluminum electrolytic
R₄	1.8kΩ 5% 1W

Prefer to upgrade Q₁ to a small-signal PNP in T0-5 package (metal can).
C₁ and C₂ are preferred in this order: polystyrene, teflon, polypropylene, …

SPICE Analysis

Correction

The spice models for this and the next analysis were incorrect on the following line:

idac 0 vin dc 6.2m ac 1 sin 0 3.9m 1kHz

The error here is that the dc current offset after the dc keyword does not count for the transient analysis, it has to be present in the sin statement as well.

I corrected the line to:

idac 0 vin dc 6.2m ac 1 sin 6.2m 3.9m 1kHz

and reran both analyses. Only the distortion results were changed.

SPICE model

Figure 2: Bode plot shows cutoff frequency slightly lower than 100kHz goal

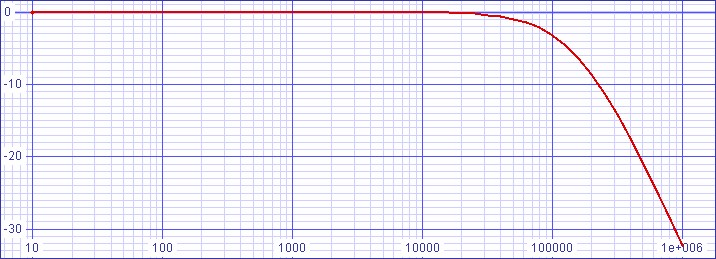Distortion results are primarily second and third harmonic

Fourier analysis for vout:
No. Harmonics: 16, THD: 0.0420128 %, Gridsize: 1024, Interpolation Degree: 3

Harmonic	Frequency	Magnitude	Norm.Mag	Percent	Decibels

1	1000	2.69196	1	100	0
2	2000	0.00111459	0.000414043	0.0414043	-67.65909107
3	3000	0.000191641	7.11902E-05	0.00711902	-82.95159574
4	4000	4.70198E-06	1.74667E-06	0.000174667	-115.1557828
5	5000	2.86806E-06	1.06542E-06	0.000106542	-119.4495831
6	6000	9.57495E-07	3.55687E-07	3.55687E-05	-128.9786402
7	7000	2.37009E-06	8.8043E-07	0.000088043	-121.1061034
8	8000	1.10266E-06	4.09612E-07	4.09612E-05	-127.7525466
9	9000	2.13659E-06	7.93694E-07	7.93694E-05	-122.0069381
10	10000	1.07911E-06	4.00865E-07	4.00865E-05	-127.9400372
11	11000	1.93559E-06	7.19026E-07	7.19026E-05	-122.8651081
12	12000	4.9167E-07	1.82644E-07	1.82644E-05	-134.7678918
13	13000	1.9412E-06	7.21108E-07	7.21108E-05	-122.8399937
14	14000	2.00793E-07	7.459E-08	0.000007459	-142.5463879
15	15000	1.45375E-06	5.40032E-07	5.40032E-05	-125.3516101

Out of curiosity, without extra current bias to Q₁ from R₂, distortion is 0.199071%.

Signal to noise ratio:
119.6568dB relative to 1V_RMS.

Relative to 2.6952V_PEAK/1.90579V_RMS at full-scale level add 5.60152dB for
125.258dB relative to 0dBFS.

Attempt at an Improvement

In my second try, setting R₅ to a very high value to allow R₃ to take a smallest possible value promises to lower distortion by allowing a design with higher bias through Q₁.

Design

The two synchronous pole frequencies will be 155.377kHz as they were calculated in equations 1 and 2 above.

Choose V_EE = 15V.
Choose V_CC = –30V to give room for desired bias.
Calculate R₃ and R₅ to convert 3.9mA input signal to 2V_RMS output signal.

(14)

R₃ || R₅ =

1.41421 × 2V

3.9mA

= 725.238Ω

Choose R₅ = 100kΩ.
Subtracting R₅ from the parallel pair R₃ || R₅ leaves R₃.

(15)

R₃ =

100kΩ × 725.238Ω

100kΩ – 725.238Ω

= 730.536Ω

Round down to nearest 1% value:
R₃ = 732Ω

Calculate R₂ for 5V headroom below ground:

(16)

I_Q1 =

30V – 5V

732Ω

= 34.153mA

(17)

I_R2 = 34.153mA – 6.2mA – 3.9mA = 24.053mA

(18)

R₂ =

15V

24.053mA

= 623.623Ω

Round to nearest 5% value:
R₂ = 620Ω

Calculate C₂ for second synchronous lowpass pole:

(19)

C₂ =

2πf_poleR_POLE

2π × 155.377kHz × (732Ω || 100kΩ)

= 1.40958nF

(20)

I_Q1-MIN =

620Ω

+ 6.2mA – 3.9mA = 26.4935mA

Then calculate maximum emitter impedance:

(21)

Z_Q1E-MIN =

25mA

26.4935mA

= 943.626mΩ

Then calculate R₁.

(22)

R₁ = 10Ω – 943.626mΩ = 9.05637Ω

Decide to round up to nearest 5% value:
R₁ = 9.1Ω

Now C₁ can be calculated.

(23)

C₁ =

2πf_poleR_POLE

2π × 155.377kHz × (943.626mΩ + 9.1Ω)

= 101.987nF

Round to nearest 5% value:
C₁ = 100nF

Calculate 1W R₄ to dissipate ½W:

(24)

R₄ =

V²

(30V – 0.7V)²

0.5

= 1.71698kΩ

Round to nearest 5% value:
R₄ = 1.8kΩ

Initially I arbitrarily choose C₃ = 47µF

Calculate C₄ for a time constant of 1s.

(25)

C₄ =

R_POLE

732Ω + 100kΩ

= 9.92733µF

Round to nearest 10% value:
C₄ = 10µF

After some thought, I realized that loading would affect the calculation of C₄ here. In the first circuit, a 10kΩ or 47kΩ load would appear insignificant in parallel with 1.43kΩ. For that reason, I originally disregarded loading there. However, here 47kΩ lowers the R₅ || R_L combination by more than a factor of 3 . Even still, raising a calculated pole from 0.1592Hz to 0.4978Hz still may not merit an alteration to the calculated value if only a 47kΩ load is expected. However for completeness, recalculating with a 47kΩ load will give a new value for C₄: 30.5766µF.

Round to nearest 10% value:
C₄ = 30µF

Parts List
Q₁	2N3906 PNP	R₅	100kΩ 5% ¼W or ½W
D₁	1N914 or 1N4148	C₁	100nF 5% plastic
R₁	9.1Ω 5% ¼W	C₂	1.3nF 5% plastic
R₂	620Ω % ½W	C₃	47µF 10% aluminum electrolytic
R₃	732Ω 1% 2W	C₄	30µF 10% plastic
R₄	1.8kΩ 5% 1W

Prefer to upgrade Q₁ to a small-signal PNP in T0-5 package (metal can).
C₁ and C₂ are preferred in this order: polystyrene, teflon, polypropylene, …
C₄ is preferred in this order: polypropylene, polycarbonate, polyester (Mylar), …

SPICE Analysis

SPICE model of improved circuit.

Figure 3: Bode plot still shows cutoff frequency slightly lower than 100kHz goal

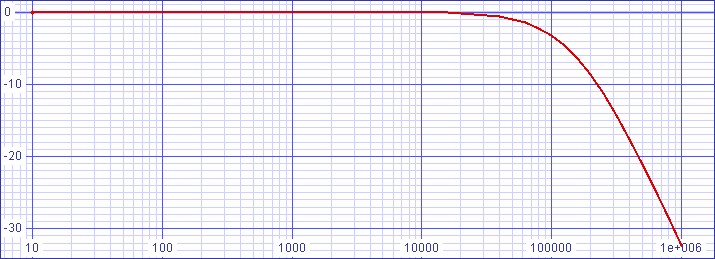Distortion results are primarily second and third harmonic
Fourier analysis for vout:
No. Harmonics: 16, THD: 0.108487 %, Gridsize: 1024, Interpolation Degree: 3

Harmonic	Frequency	Magnitude	Norm.Mag	Percent	Decibels

1	1000	2.71265	1	100	0
2	2000	0.00293561	0.00108219	0.108219	-59.31392967
3	3000	0.000206089	7.59733E-05	0.00759733	-82.38678018
4	4000	0.000010125	3.7325E-06	0.00037325	-108.5600037
5	5000	4.86714E-06	1.79424E-06	0.000179424	-114.9223893
6	6000	6.40395E-08	2.36078E-08	2.36078E-06	-152.5388897
7	7000	5.0589E-06	1.86493E-06	0.000186493	-114.5867493
8	8000	6.24975E-08	2.30393E-08	2.30393E-06	-152.7506144
9	9000	4.0545E-06	1.49467E-06	0.000149467	-116.5090936
10	10000	4.22788E-07	1.55858E-07	1.55858E-05	-136.145418
11	11000	2.47042E-06	9.10705E-07	9.10705E-05	-120.8124456
12	12000	3.31809E-07	1.22319E-07	1.22319E-05	-138.2501216
13	13000	1.05783E-06	3.89963E-07	3.89963E-05	-128.1795319
14	14000	6.45024E-07	2.37784E-07	2.37784E-05	-132.4763474
15	15000	4.6302E-07	1.70689E-07	1.70689E-05	-135.3558893

Signal to noise ratio:
117.8938dB relative to 1V_RMS.

Relative to 2.72627V_PEAK/1.92776V_RMS at full-scale level add 5.70108dB for
123.595dB relative to 0dBFS.

Result of Change

Paradoxically, the improvement has increased the distortion. I believe this result is due to distortion having some inversely proportional relationship to the value of R₂ as well at to the current bias change. Because primarily the second harmonic was raised leaving the third harmonic the same this change becomes a more euphonic preference. Perhaps even more important the change allows the use of a lower distortion capacitor at C₄ . The second circuit is not recommended to drive loads lower than 47kΩ.

Design an NPN circuit

Figure 4: Schematic of single-ended analog circuit

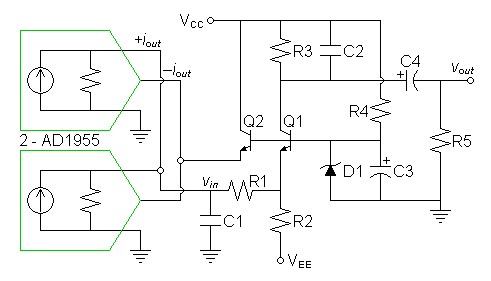Note: Only left channel shown. Duplicate for the right channel.

This NPN circuit is only flipped in polarity from the PNP circuit first introduced apart from two details: That this circuit is biased with a zener rather than an normal diode because the particular DAC requires its current output to sink into a non-zero voltage and the decision to use two DACs.

Evaluate Datasheet

The datasheet for the AD1955 gives the following output specifications:

AC output		8.64mA peak-to-peak differential 2.16mA peak single ended
DC offset		–3.24mA (specified as current sink)
Output impedance		Unspecified
Analog sink voltage		2.80V ideal, down to low of 2.39V

Analyzing polarity of reference analog circuit suggests no polarity reversal for connection. Because the output current specifications are expected to design to a high output impedance, use two parallel devices.

As a parallel pair their specifications are now:

AC output		17.28mA peak-to-peak differential 4.32mA peak single ended
DC offset		-6.48mA (specified as current sink)
Output impedance		Unspecified
Analog sink voltage		2.80V ideal, down to low of 2.39V

Design

Begin by calculating two synchronous pole frequencies which together will roll off at 100kHz:

(26)

α =

² 2

–1

=0.643594

(27)

f_stage =

f_system

100kHz

0.643594

= 155.377kHz

Choose V_EE = –15V
Choose V_CC = 30V to give room for desired bias.
Assume rated output current is dropped between the optimal output sink voltage and ground. Then calculate DAC output impedance:

(28)

R_DAC =

V_SINK – GND

I_DAC-MAX

2.8V - 0V

6.48mA + 4.32mA

= 259.259Ω

Note: This DAC has no R-2R resistor ladder determining its output current that any certainty could be attributed to this output impedance. It could have open collector/drain outputs instead of resistive. However removing R_DAC in the simulation does not seem to significantly alter the final simulation results.

Calculate D₁ zener voltage

(29)	V_zener-D1 = 2.8V + 0.7V = 3.5V

Round down to nearest 5% value to bracket new sink voltage to 2.39V–2.8V range.
V_zener-D1 = 3.3V
Operating sink voltage will now be:
.V_SINK = 2.6V

Calculate R₃ and R₅ to convert 3.9mA input signal to 2V_RMS output signal

(30)

R₃ =

2 × 1.41421 × 2V

4.32mA

= 1.30946kΩ

Round up to nearest 1% value:
R₃ and R₅ = 1.33kΩ
Here, I decided to round up to compensate for the slight loss of signal current to the current divider created by R_DAC and R₁.

Calculate R₂ for 5V headroom below ground:

(31)

I_Q1 =

30V - 5V - 3.3V

1.33kΩ

= 16.3158mA

(32)

I_R2 = 16.3158mA - 6.48mA - 2.16mA = 7.67579mA

(33)

R₂ =

15V + 2.6V

7.67579mA

= 2.29292kΩ

Round up to nearest 5% value:
R₂ = 2.4kΩ

Calculate C₂ for second synchronous lowpass pole:

(34)

C₂ =

2πf_poleR_POLE

2π × 155.377kHz × (1.33kΩ/2)

= 1.54032nF

Round down to nearest 5% value:
C₂ = 1.5nF

To prepare to calculate for first lowpass pole, calculate an R₁ value to add with the AC emitter impedance to total about 10Ω.
First calculate minimum emitter current.

(35)

I_Q1-MIN =

15V + 2.6V

2.4kΩ

+ 6.48mA - 4.32mA = 9.49333mA

Then calculate maximum emitter impedance:

(36)

Z_Q1E-MIN =

25mV

9.49333mA

= 2.63343Ω

Then calculate R₁.

(37)

R₁ = 10Ω – 2.63343Ω = 7.36657Ω

Decide to round up to nearest 5% value:
R₁ = 7.5Ω

Now C₁ can be calculated.

(38)

C₁ =

2πf_poleR_POLE

2π × 155.377kHz × (2.63343Ω + 7.5Ω)

= 101.083nF

Round to nearest 5% value:
C₁ = 100nF

Calculate 1W R₄ to dissipate ½W:

(39)

R₄ =

V²

(30V – 3.3V)²

0.5

= 1.42578kΩ

Round up to nearest 5% value:
R₄ = 1.5kΩ

Arbitrarily chose C₃ = 47µF.

Calculate C₄ for a time constant of 1s.

(40)

C₄ =

R_POLE

1.33kΩ + 1.33kΩ

= 375.94µF

Round to nearest 10% value:
C₄ = 390µF

Parts List
Q₁,Q₁	2N3904 PNP	R₅	1.33kΩ 1% ½W or 1W
D₁	3.3V zener	C₁	100nF 5% plastic
R₁	7.5Ω 5% ¼W	C₂	1.5nF 5% plastic
R₂	2.4kΩ % ½W	C₃	47µF 10% aluminum electrolytic
R₃	1.33kΩ 1% 1W	C₄	390µF 10% aluminum electrolytic
R₄	1.5kΩ 5% 1W

Prefer to upgrade Q₁ to a small-signal NPN in T0-5 package (metal can).
C₁ and C₂ are preferred in this order: polystyrene, teflon, polypropylene, …

SPICE Analysis

SPICE model

Figure 5: Bode plot still shows cutoff frequency slightly lower than 100kHz goal

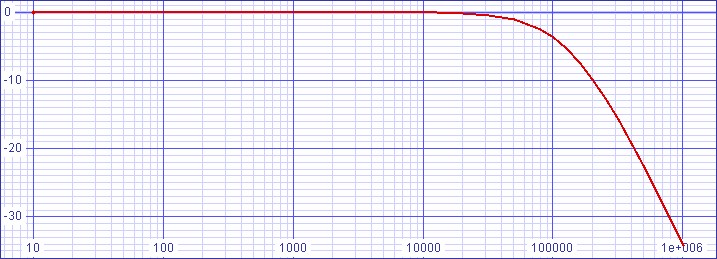Fourier analysis for vout:
No. Harmonics: 16, THD: 0.0415427 %, Gridsize: 1024, Interpolation Degree: 3

Harmonic	Frequency	Magnitude	Norm. Mag	Percent	Decibels

1	1000	2.847	1	100	0
2	2000	0.00117564	0.000412941	0.0412941	-67.6822
3	3000	0.000128299	4.50648E-05	0.00450648	-86.9233
4	4000	1.39636E-05	4.90466E-06	0.000490466	-106.188
5	5000	4.21864E-06	1.48179E-06	0.000148179	-116.584
6	6000	5.05001E-07	1.7738E-07	0.000017738	-135.022
7	7000	2.64547E-06	9.29215E-07	9.29215E-05	-120.638
8	8000	1.00591E-06	3.53324E-07	3.53324E-05	-129.037
9	9000	1.88327E-06	6.61494E-07	6.61494E-05	-123.589
10	10000	7.95153E-07	2.79295E-07	2.79295E-05	-131.079
11	11000	1.15167E-06	4.0452E-07	0.000040452	-127.861
12	12000	1.5341E-07	5.38848E-08	5.38848E-06	-145.371
13	13000	1.31741E-06	4.62736E-07	4.62736E-05	-126.693
14	14000	2.86087E-07	1.00487E-07	1.00487E-05	-139.958
15	15000	1.11035E-06	3.90009E-07	3.90009E-05	-128.179

Signal to noise ratio:
122.0053dB relative to 1V_RMS.

Relative to 2.847V_PEAK/2.01313V_RMS at full-scale level add 6.07745dB for
128.083dB relative to 0dBFS.

Document History
December 1, 2012 Created.
December 1, 2012 Added equation numbers to design and some extra text and rescinded 750µF calculation for C₃.
December 1, 2012 Added a second design sequence aimed to improve distortion.
December 2, 2012 Added text recalculating a new C4 value for the second circuit under load.
December 4, 2012 Corrected 25mA in equation 9 to 25mV.
December 7, 2012 Correcting SPICE model error changed distortion results somewhat. Reworded statement about useful DACs to indicate that the AD1955 will require an NPN design. Added paragraph on the interpretation of the datasheet.
January 1, 2013 Added an NPN design and analysis based on the AD1955.
January 2, 2013 Changed schematics to show how unused DAC outputs should be terminated.