Apples and Oranges

A Simple Proof that Class-A and Class-B Distortion Specifications Are not Comparable

Introduction

Traditional standards for specifying amplifier distortion require specification at maximum rated RMS power. By these standards, it seems odd that higher distortion class-a amplifiers can subjectively sound clearer than lower distortion class-b¹ amplifiers of the same power. Lets do the math and find out what is behind this seeming discrepancy.

Class A Analysis

Class A distortion is due entirely to transfer curve shape. Because polynomials can be fitted to any curve, a transfer curve could be represented by the following polynomial:

(1)	\|H(v)\| = k₀ + k₁v + k₂v²+ k₃v³ + k₄v⁴ + ... + k_nvⁿ + ... + k_∞v^∞

Also consider that for many reasons the second order term could reasonably presumed to dominate the characteristic polynomial:

Euphonic design tends to emphasize the second order term.
Individual transistor curves contributing to transfer curves are predominantly second order.²

For simplicity, presume a second order error only for the signal+error voltage equation:

(2)	\|H(v)\| = v + kv²

Divide error by signal to get relation of distortion to voltage:

(4)

Dist(v) =

kv²

= kv

Where

(5)

v =

Make substitution to show relation of distortion to power

(6)

Dist(P) = k

Figure 1: Class A distortion rises with power until onset of saturation

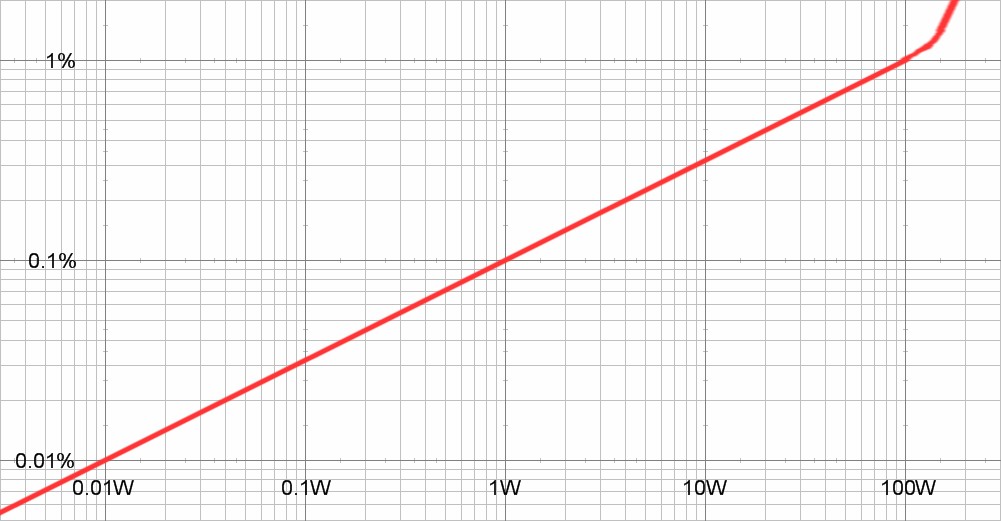Class B Analysis

Class B distortion tends to be at a fixed level without regard to signal magnitude because crossover distortion dominates that of the overall transfer curve. (Think of crossover distortion as a fixed distortion region unchanged by signal magnitude.) Therefore distortion decreases as power level is increased.

Approximate signal+error voltage equation with fixed error k:

(7)	\|H(v)\| = v + k

Divide error by signal to get relation of distortion to voltage:

(8)

Dist(v) =

Given

(9)

v =

Make substitution to show relation of distortion to power:

(10)

Dist(P) =

Figure 2: Class B distortion declines with power until onset of saturation

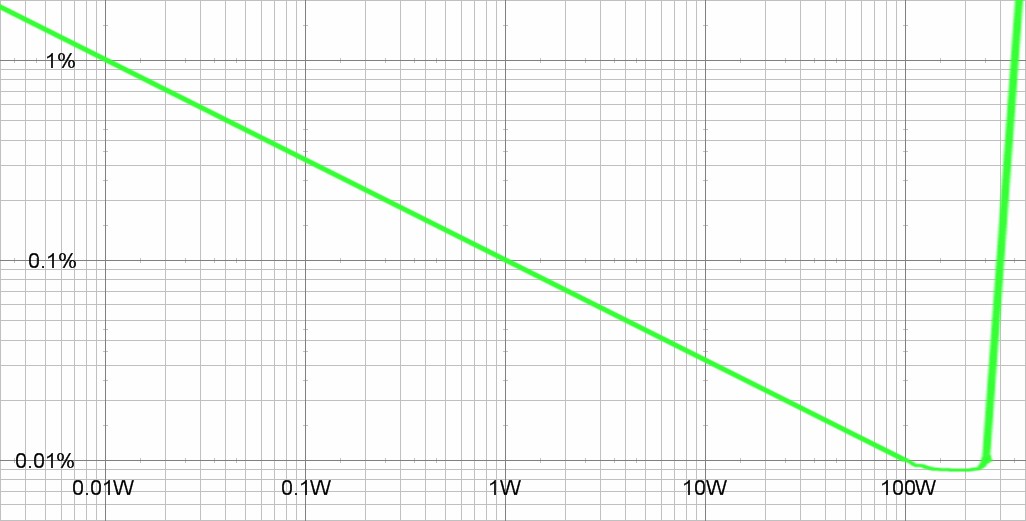Deductions

Figure 3: Comparison of distortion profiles

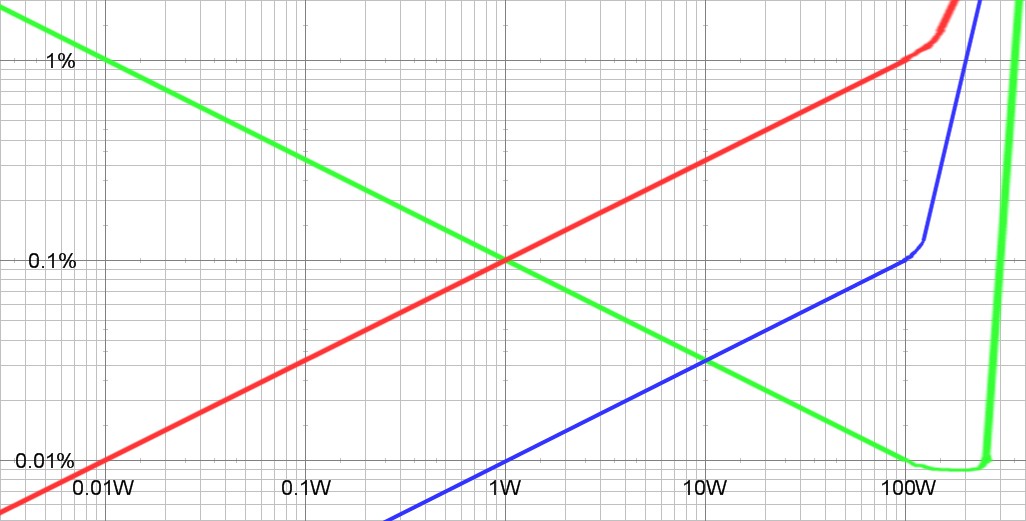Distortion profile legend:

Green: Class-b amplifier specified at 0.01% distortion at 100W_RMS.
Red: Somewhat euphonic class-a amplifier specified at 1% distortion at 100W_RMS.
Blue: A more neutral class-a amplifier specified at 0.1% distortion at 100W_RMS.

Since distortion varies with power level, it becomes obvious that distortion specified at maximum power favors class B amplifiers. Because speaker efficiencies average about 89dB/W, the distortion of ordinary listening done at power levels of only a few watts is not represented by maximum power distortion specifications.

From the graph above, the euphonic amplifier has as low distortion as the lower distortion class-b amplifier at the important 1W level. The neutral class-a amplifier excels the lower distortion class-b amplifier everywhere below 10W.

Other observations are to be made as well.

Because class-a distortion diminishes with level, class-a has a clearer window to the smallest musical details that class-b cannot show.
Because distortion adds apparent brightness, the effect differing with frequency, increasing distortion with magnitude in class-a amplifiers may create an impression of dynamic range expansion, whereas the inverse relationship in the class-b amplifier may create an impression of dynamic range compression instead.
Natural distortion processes, as internal to musical instruments and even in the nonlinear compressibility or compliance of air, are the same in nature as class-a distortion. The human brain might be expected to be more accepting of natural distortion tendencies than contradictory ones, perhaps perceiving them to be more pleasing.
Listening habits may chose an amplifier class having the least distortion at the listener's normal listening level. Thus the classical listener listening to many soft passages in the context of a wide dynamic range may lean toward class-a while those preferring highly compressed and perhaps loud music find no fault listening to his class-b amplifier. (This is a much more subjective and less certain statement than the rest.)

Be careful however using this information to interpret actual distortion measurements to determine the class of an amplifier of unknown topology. Because real distortion measurements include noise and because constant noise would appear to have a declining profile with magnitude as crossover distortion, class-a plots will show class-b characteristics at power levels where the noise level is higher than the distortion.

In the end, I may only be entertaining you with ideas that most of you already know.

¹I use class-b here as optimally biased and not operating for any range in class-a which I deem class-ab.

²It is well known that FETs and vacuum tubes have square law distortion characteristics. Less obvious the BJT.

The exponential in the Ebers-Moll equation I_E = I_EO(e^40V - 1) is well known for its Maclaurin series:

e^x = 1 + x +

x²

x³

x⁴

+ ... +

xⁿ

+ ...

, where n! is the product of all the number from 1 to n.

This equation holds the potential for a high order error term especially as the voltage in the exponent is multiplied by 40/V (= 1/V_T ≈ 1/25mV). Fourier analysis shows progressively greater suppression of higher order harmonics with increased bias and local feedback until the second harmonic becomes dominant.

Document History
October 2, 2011 Created.